Эксперимент в замкнутом контуре

С помощью этой процедуры предполагается, что нет модели процесса. Процедура основана только на измерении. Эксперимент может быть проведен с устойчивыми и неустойчивыми процессами. Система с замкнутым контуром тестируется с P контроллером (интеграл и производная отключаются). Коэффициент усиления P контроллера увеличивают, пока система не достигнет запаса устойчивости (перейдёт в режим колебаний). Когда колебания с постоянной амплитудой и периодом устанавливаются, то можно определить период колебания Т_u (критическая величина) и (критический коэффициент усиления контроллера K_u. В ходе эксперимента, при изменении уставки, можно определить статический коэффициент усиления K_p как отношение изменений ответа и уставки в стабильном состоянии.

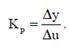
На основании экспериментально полученных Т_u и K_u Циглер и Никольс дали
следующие таблицы параметров контроллера (если критерий - quarter decay ratio):

Получить произведение c = K_pK_u . Его можно трактовать как максимальный (критический) коэффициент усиления разомкнутой системы и использовать для определения настроечных параметров.

Как правило, рекомендуется использовать настройки параметров Циглера-Никольса:
1. Если c = K_pK_u <2, то законы управления, которые могут компенсировать транспортные задержки, должны быть использованы.

2. Если c> 20, то лучшие результаты могут быть достигнуты более сложным алгоритмом
управления.
3. Если 1,5 < c <2, то PID-регулятор может быть использован, если требования к эффективности системы управления не очень строгие. Для достижения хорошей производительности настройки Циглера-Николса должны быть изменены.

4. Если c <1,5, то PI контроллер можно попробовать, если требования к эффективности системы управления не являются очень строгими. Дифференциальный режим не будет значительно использован. Другие структуры также могут быть рекомендованы.

Метод Ziegler-Nichols (Циглера Никольса) - Настройка по методу максимального коэффициента усиления. Этот способ применяется, если допустим колебательный процесс, при котором значения регулируемой величины значительно выходят за пределы задания (на рис. задание - U).

Алгоритм настройки:

1) определяется предельный коэффициент К_мах усиления при котором система переходит в колебательный режим, т.е. без интегральной и дифференциальной части (Т_D=0, Т_Ґ =0). Вначале К=0, затем он увеличивается до тех пор, пока система переходит в колебательный режим. Управление соответствует схеме P-регулятора.

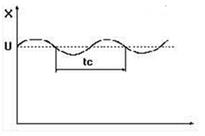
Рис. 5 Настройка по методу максимального коэффициента усиления

2) определяется период колебаний t_c (см. рис. 5).

3) вычисляются коэффициенты настройки согласно следующим примерным соотношениям:

для P -регулятора К= 0.5·Kмах

для PD -регулятора К= 0.5·Кмах, T_D=0.05·tc

для PI -регулятора К= 0.45·Кмах, T_I = 0.8·tс

для PID -регулятора К= 0.6·Кмах, T_I = 0.5·tс, T_D=0.12·tc.

2. Правила оптимизации согласно Chien, Hrones и Reswick.

Правила оптимизации для систем с компенсацией (без перерегулирования). Пример дляPID- контроллера.

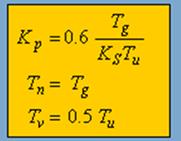
Рис. 6 Правила оптимизации для систем без перерегулирования.

Правила оптимизации для систем с компенсацией (с перерегулированием). Пример для PID- контроллера

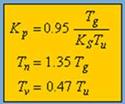
Рис. 7 Правила оптимизации для систем с перерегулированием.

Используя принципы оптимизации согласно Chein, Hrones и Reswick, возможно внести изменения, чтобы:

• установить желательный ответ контура (лучший ответ на изменение setpoint или хороший ответ на возмущения)
• задать желательную тенденцию колебания контура (с/без перерегулирования управляемой переменной).