Проверить наличие гетероскедастичности в модели. Объяснить полученные результаты.

Если остатки имеют постоянную дисперсию, они называются гомоскедастичными, но если они непостоянны, то гетероскедастичными. Гетероскедастичность приводит к тому, что коэффи­циенты регрессии больше не представляют собой лучшие оценки или не являются оценками с минимальной дисперсией, следова­тельно, они больше не являются наиболее эффективными коэф­фициентами.

Воздействие гетероскедастичности на оценку интервала прогнозирования и проверку гипотезы заключается в том, что хотя коэффициенты не смещены, дисперсии и, следовательно, стандартные ошибки этих коэффициентов будут смещены. Если смещение отрицательно, то оценочные стандартные ошибки бу­дут меньше, чем они должны быть, а критерий проверки будет больше, чем в реальности. Таким образом, мы можем сделать вывод, что коэффициент значим, когда он таковым не является. И наоборот, если смещение положительно, то оценочные ошиб­ки будут больше, чем они должны быть, а критерии проверки – меньше. Значит, мы можем принять нулевую гипотезу, в то вре­мя как она должна быть отвергнута.

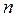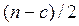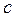Проверкой на гетероскедастичность служит тест Голдфелда-Кванта. Он требует, чтобы остатки были разделены на две груп­пы из наблюдений, одна группа с низкими, а другая – с высо­кими значениями. Обычно срединная одна шестая часть наблю­дений удаляется после ранжирования в возрастающем порядке, чтобы улучшить разграничение между двумя группами. Отсюда число остатков в каждой группе составляет , где пред­ставляет одну шестую часть наблюдений.

Критерий Голдфелда-Кванта – это отношение суммы квадра­тов отклонений (СКО) высоких остатков к СКО низких остатков:

.

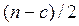Этот критерий имеет 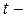распределение с 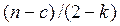степе­нями свободы.

Чтобы решить проблему гетероскедастичности, нужно иссле­довать взаимосвязь между значениями ошибки и переменными и трансформировать регрессионную модель так, чтобы она отра­жала эту взаимосвязь. Это может быть достигнуто посредством регрессии значений ошибок по различным формам функций пе­ременной, которая приводит к гетероскедастичности, например,

,

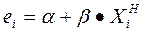где 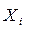- независимая переменная (или какая-либо функция не­зависимой переменной), которая предположительно является причиной гетероскедастичности, а 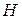отражает степень взаимо­связи между ошибками и данной переменной, например, 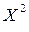или 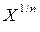и т. д.

Следовательно, дисперсия коэффициентов запишется:

.

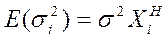Отсюда если 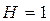, мы трансформируем регрессионную мо­дель к виду:

.

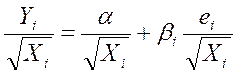Если 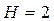, т.е. дисперсия увеличивается в пропорции к квадрату рассматриваемой переменной 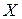, трансформация при­обретает вид:

.

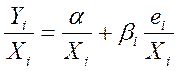Используя Eviews, можно провести проверку и устранение гетероскедастичности следующим образом:

Ø Запустить стандартную регрессию.

Ø Вычислить остатки.

Ø Запустить регрессию с использованием квадрата остатков как зависимой переменной и оценить зависимую переменную 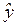как независимую переменную (тест White).

Ø Оценить nR², где n – объем выборки, R² – коэффициент детерминации.

Ø Использовать статистику 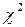с одной степенью свободы (в EVIEWS – используется F – статистика) для проверки существенности отличия nR² от нуля.

Ø Основным способом устранения гетероскедастичности является применение взвешенного метода наименьших квадратов.

Выбираем тест White (см. рис. 64).

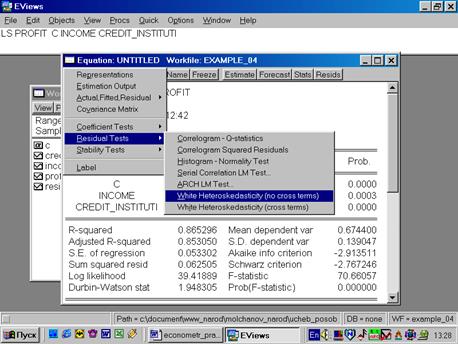
Рис. 64.

Итог формы вывода представлен на рис. 65.

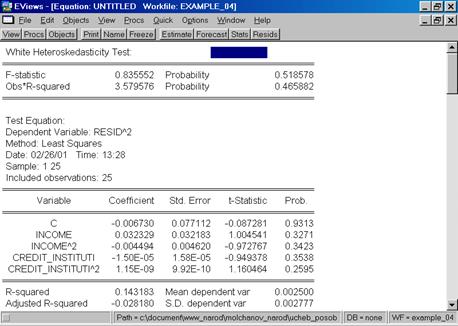
Рис. 65.

Как следует из приведенной распечатки, вероятность ошибки первого рода равна 51,86%. Следовательно, нулевую гипотезу (об отсутствии гетероскедастичности) нельзя отклонить.

Для случая, когда гетероскедастичность присутствует, проблему гетероскедастичности можно решать следующим образом:

Выбираем в пунктах меню текущего окна опцию Proc/Specify/Estimate… (рис. 66). Появляется окно оценки регрессии, где необходимо нажать клавишу Optionsи в появившимся окне отметить Heteroskedasticity (рис. 67).

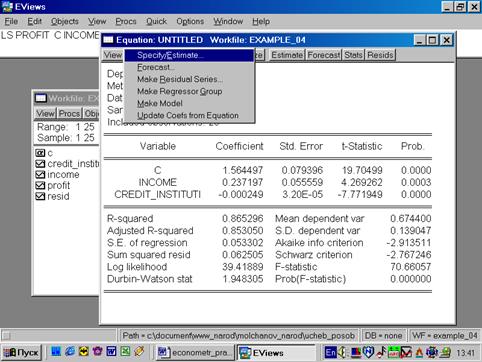
Рис. 66.

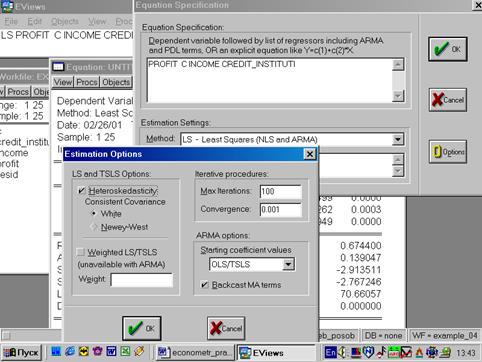
Рис. 67.

Появилось новое, переоцененное уравнение (рис. 68). Полученное уравнение можно вновь проверить по тесту White.

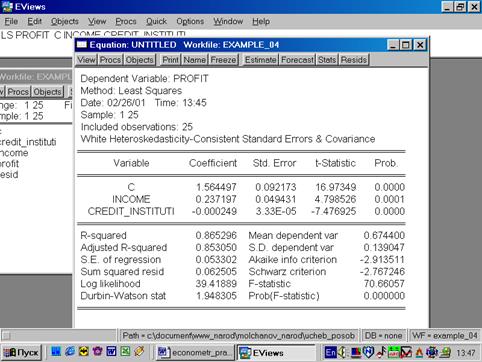
Рис. 68.