ВНИМАНИЕ!!! Все файлы, созданными Вами во время практического занятия, необходимо сохранять на личных дискетах (желательно в двух экземплярах на разных носителях).
Практическое занятие № 2.
«Применение Eviews при построении и анализе линейной однофакторной модели регрессии»
Пример 2. Имеются следующие данные по 10 фермерским хозяйствам области:
| № п\п | ||||||||||
| Урожайность зерновых ц\га | ||||||||||
| Внесено удобрений на 1 га посевов, кг | 4,0 | 2,5 | 5,0 | 5,8 | 7,5 | 5,7 | 7,0 | 3,0 | 6,0 | 3,5 |
Необходимо:
1. Создать файл с исходными данными в среде Excel (файл example_02.xls).
2. Осуществить импорт исходных данных в Eviews.
3. Создать workfile (рабочий файл).
4. Найти значения описательных статистик по каждой переменной и объяснить их.
5. Построить поле корреляции моделируемого (результативного) и факторного признаков. Объяснить полученные результаты.
6. Найти значение линейного коэффициента корреляции и пояснить его смысл.
7. Определить параметры уравнения парной регрессии и интерпретировать их. Объяснить смысл полученного уравнения регрессии.
8. Оценить статистическую значимость коэффициента регрессии 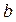 и уравнения в целом. Сделать выводы.
и уравнения в целом. Сделать выводы.
9. Объяснить полученное значение 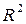 .
.
10. Построить эмпирическую и теоретическую линию регрессии и объяснить их.
11. Построить и проанализировать график остатков.
12. С вероятностью 0,95 построить доверительный интервал для ожидаемого значения урожайности 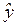 по точечному значению
по точечному значению 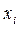 .
.
13. Оформить отчет по занятию.
Порядок выполнения задания
1. В Excel исходные данные должны быть организованы таким образом, чтобы в каждой колонке были представлены данные по соответствующей переменной (рис. 21). Имена переменных набираются латинскими буквами. Файл необходимо сохранить в формате Excel 5.0/95 (рис. 22). Введем обозначения: урожайность зерновых – переменная Productivity(зависимая, Y); внесено удобрений на 1 га посевов – Fertilizers(независимая, X).
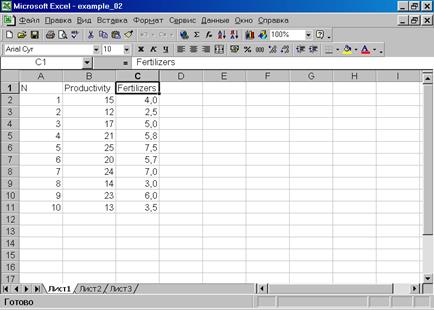
Рис. 21.
Рис. 22.
2. Создаем рабочий файл для импортирования исходных данных из Excel в Eviews, работая с диалоговым окном File/New/Workfile(рис. 23), далее выбираем: Procs/Import/Read Text-Lotus-Excel(рис. 24).
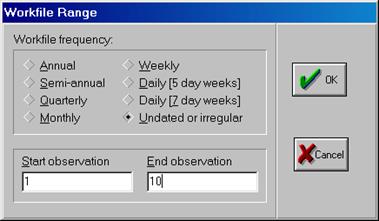
Рис. 23.
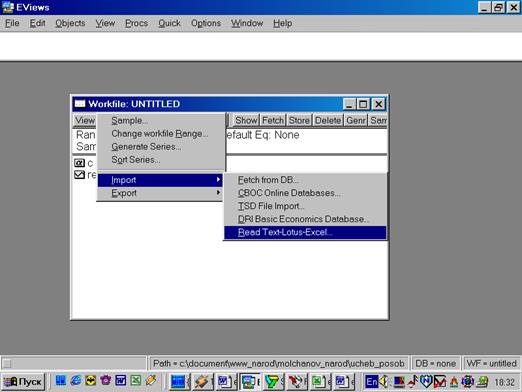
Рис. 24.
3. Далее в открывшемся окне находим и выбираем файл Excel с исходными данными (файл не должен в этот момент использоваться любыми программами), осуществляя автоматический импорт исходных данных в workfile (рис. 25). В следующем открывшемся диалоговом окне нужно указать адрес ячейки, в которой записаны данные первого по счету наблюдения и число переменных в рассматриваемом примере (рис. 26).. Если все выполнено правильно, то в открывшемся окне workfile должны появиться имена переменных, а также константа (с) и остатки (resid) (рис. 27).
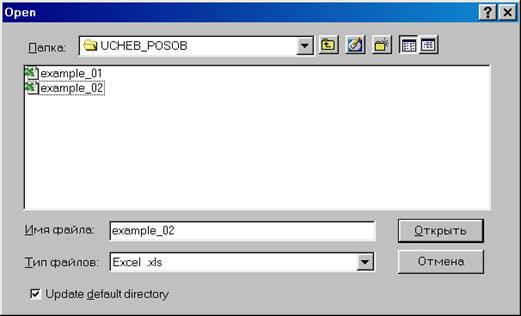
Рис. 25.
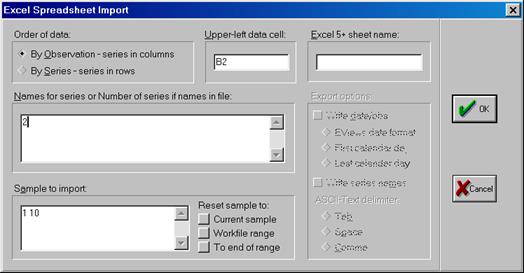
Рис. 26.
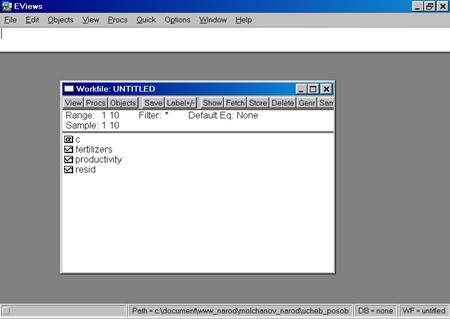
Рис. 27.
Рис. 28.
Сохраним рабочий файл (рис. 28).
4. Значения описательных статистик находим следующим образом: в окне workfile выделяем переменные, щелкаем мышкой по выделенной части и далее выбираем: Open/As Group/(рис. 29). Открывается окно с исходными данными. Новую группу можно сохранить, выбрав опцию Name(рис. 30). Для просмотра описательных статистик View/Descriptive Stats/Common Sample (рис 31). Результат представлен на рис. 32.
Рис. 29.
Рис. 30.
Рис. 31.
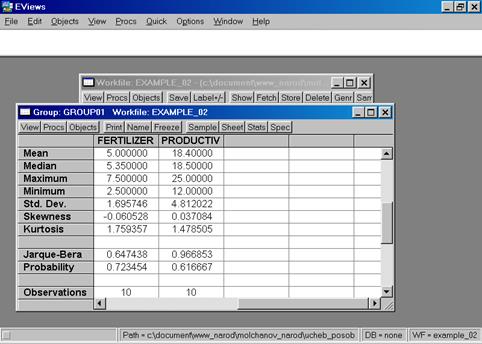
Рис. 32.
5. В окне workfile (рис. 32) для построения поля корреляции необходимо выбрать следующие пункты меню: VIEW/GRAPH/SCATTER/SIMPLE SCATTER/ (рис. 33). Полученный в результате график представляет собой поле корреляции результативного и факторного признаков (рис. 34).
6. В окне Workfile (используя созданную группу из двух переменных) выбрать: /VIEW/CORRELATION/(рис. 35). Полученная таблица - корреляционная матрица, в которой отражено значение коэффициента парной корреляции результативного и факторного признаков (рис. 36).
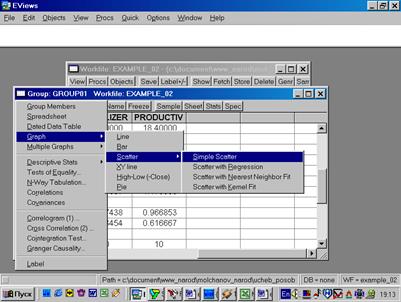
Рис. 33.
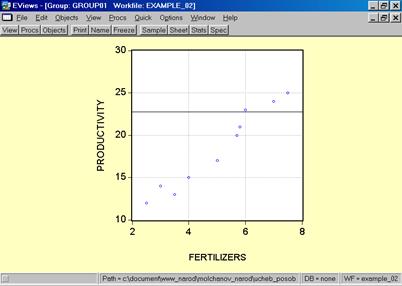
Рис. 34.

Рис. 35.
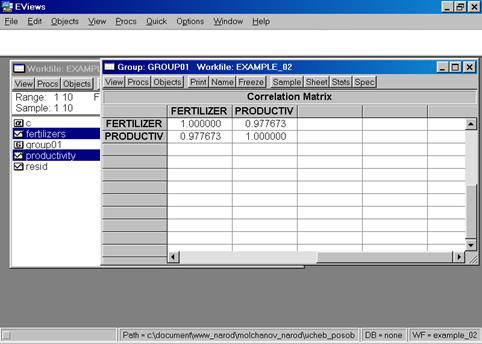
Рис. 36.
7. В диалоговом окне описать в общем виде искомое уравнение: LS PRODUCTIVITY C FERTILIZERS <Enter> (метод наименьших квадратов (LS) эндогенная переменная, константа, экзогенная переменная), или выбрать в строке главного меню EVIEWS: QUICK/ESTIMATE EQUATION/ PRODUCTIVITY C FERTILIZERS (рис. 37). В открывшемся окне (рис. 38) должны быть переменные: зависимая переменная, применяемый метод, число наблюдений, параметры уравнения регрессии, стандартные ошибки, значения t – статистик и соответствующие им вероятности, значение 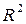 и ряд других показателей.
и ряд других показателей.
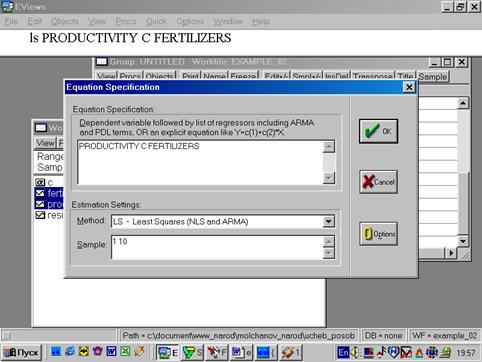
Рис. 37.
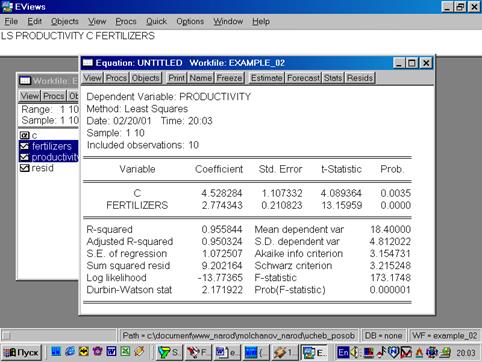
Рис. 38.
8. и 9. Результаты выполнения п.7 позволяют оценить статистическую значимость параметров уравнения регрессии и объяснить полученное значение R  .
.
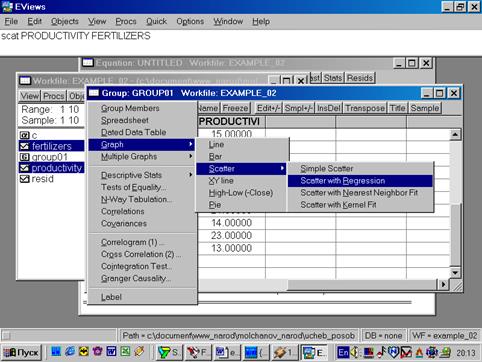
Рис. 39.
10. Для построения эмпирической линии регрессии в окне workfile выделить группу переменных и выбрать: VIEW/GRAPH/SCATTER/SCATTER WITH REGRESSION/(рис. 39). В промежуточном окне (рис. 40) необходимо нажать <Ok>. Полученный график (рис. 41) – эмпирическая линия регрессии. Чтобы построить теоретическую (подогнанную) линию регрессии, необходимо найти теоретические (вычисленные с помощью уравнения регрессии) значения результативного признака. Для этого открыть окно с параметрами уравнения регрессии, далее выбрать Forecast(рис. 42). Появится окно (рис. 43), в котором к исходным добавилась новая переменная PRODUCTIVIf(прогнозное, (теоретическое, выровненное) значение переменной PRODUCTIVITY). Затем, выделив все переменные (включая теоретическое значение результативного признака), в командной строке записать SCAT FERTILIZERS PRODUCTIVITY PRODUCTIVIf. Полученный график (рис. 44) – теоретическая (подогнанная) линия регрессии.
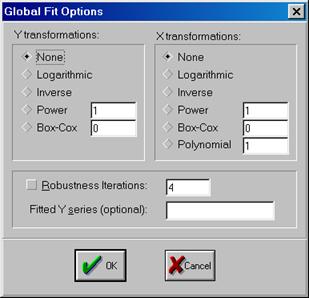
Рис. 40.
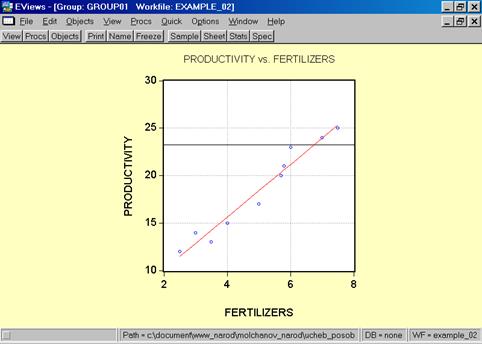
Рис. 41.
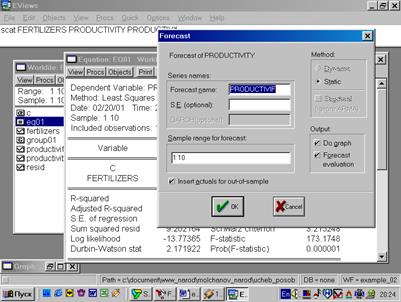
Рис. 42.
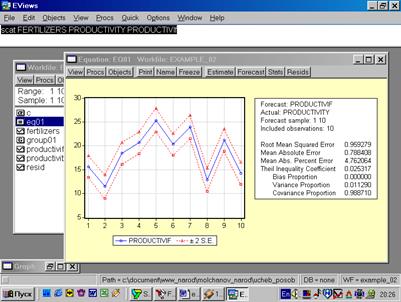
Рис. 43.
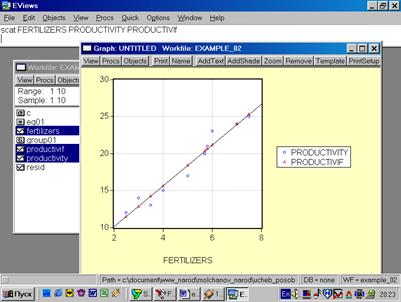
Рис. 44.
11. Данная операция возможна только в том случае, если ей предшествует построение регрессионного уравнения. В окне Workfile можно дважды щелкнуть на переменной Resid(рис. 45). Далее, выбрать: VIEW/LINE GRAPH/, или, открыв окно с параметрами уравнения регрессии, выбрать: VIEW /ACTUAL, FITTED…/ACTUAL, FITTED…TABLE/(рис. 46). Результат представлен на рис. 47. Другой вариант вывода (фактические, предсказанные значения переменных, остатки, график остатков) – рис. 48.
Рис. 45.

Рис. 46.
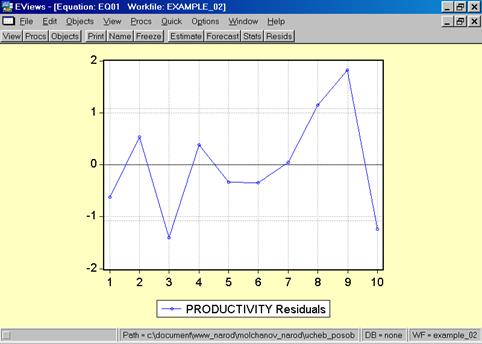
Рис. 47.
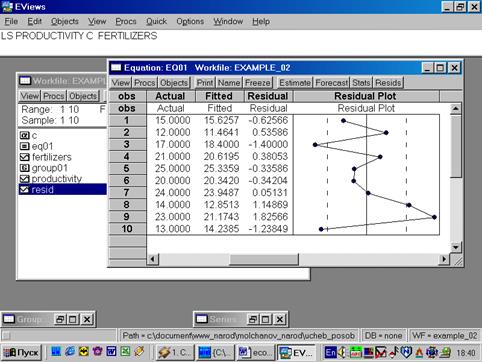
Рис. 48.
12. Для нахождения границ доверительного интервала в командной строке необходимо указать (рис. 49):
GENR XK = 5 * 1.05
GENR YFK = 4.53 +2.77*XK
GENR h = ((1 + 0.25^2)/1.6957^2) ^0.5
GENR CI = 2.31*(1.07/10^0.5)*h
В результате искомые границы определяются следующим образом:
YFK 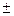 CI , т.е. от YFK+CI до YFK-CI (см. рис. 50).
CI , т.е. от YFK+CI до YFK-CI (см. рис. 50).
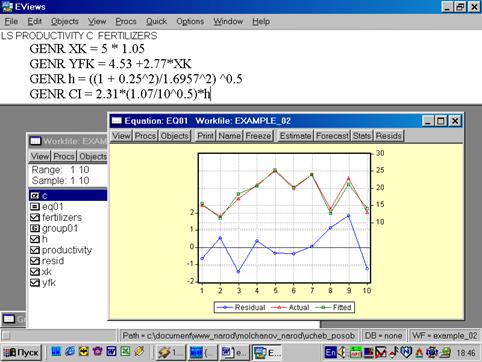
Рис. 49.
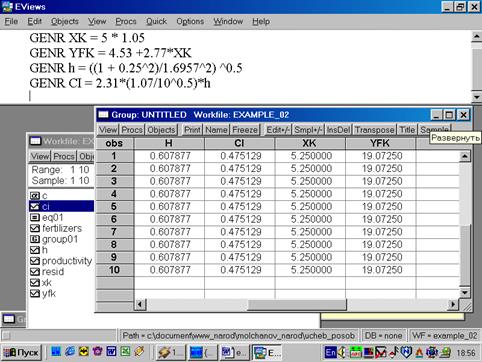
Рис. 50.
13. Оформить отчет по занятию.
Отчет должен содержать: подробные пояснения расчетов, ссылки на используемые формулы, результаты работы Eviews в виде экранных копий, другую, необходимую на Ваш взгляд, информацию.
Практическое занятие № 3.
«Применение Eviews при построении и анализе линейной однофакторной модели регрессии»
Дата добавления: 2015-08-11; просмотров: 1734;
