Оформить отчет.
Практическое занятие № 5.
«Фиктивные переменные»
Иногда необходимо включение в регрессионную модель одной или более качественных переменных (например, разделение по полу: мужской и женский; по уровню образования: общее и профессиональное и т.д.). Альтернативно может понадобиться сделать качественное различие между наблюдениями одних и тех же данных. Так, если проверяется взаимосвязь между размером компании и месячными доходами по акциям, может быть желательным включение качественной переменной, представляющей месяц январь, по причине хорошо известного «январского эффекта» во временных рядах доходов по ценным бумагам. Данный «январский эффект» - это феномен, заключающийся в том, что средние доходы по акциям, особенно небольших компаний, в среднем выше в январе, чем в другие месяцы. Таким образом, если мы рассматриваем январские наблюдения как качественно отличные от других наблюдений, фиктивная переменная 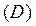 позволит произвести подобное качественное различие.
позволит произвести подобное качественное различие.
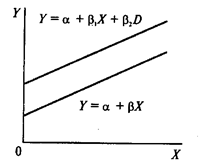
Фиктивные переменные бывают двух типов -сдвига и наклона. Фиктивная переменная сдвига - это переменная, которая меняет точку пересечения линии регрессии с осью ординат в случае применения качественной переменной (рис. 69). Фиктивная переменная наклона - это та переменная, которая изменяет наклон линии регрессии в случае использования качественной переменной (рис. 70). Оба типа фиктивных переменных будут иметь значение 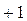 или
или  , когда наблюдения данных совпадают с уместной количественной переменной, но будут иметь нулевое значение при совпадении с наблюдениями, где эта качественная переменная отсутствует.
, когда наблюдения данных совпадают с уместной количественной переменной, но будут иметь нулевое значение при совпадении с наблюдениями, где эта качественная переменная отсутствует.
| 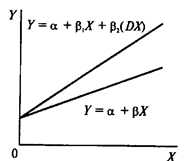
| |
| Рис. 69. | Рис. 70. |
Пример 5. По данным примера 1 (файлexample_01.xls.) дать интерпретацию бинарным, «фиктивным» переменным, принимающим значения 0 или 1: floor – принимает значение 0, если квартира расположена на первом или последнем этаже, cat –принимает значение 1, если квартира находится в кирпичном доме.
Построим регрессионное уравнение видаLS PRICE C CAT FLOOR (рис 71). Тем самым мы предполагаем (хотя в действительности это может быть и не так), что на цену квартиры оказывают влияние только две, указанные выше, составляющие. В результате получится уравнение следующего вида (рис 72):
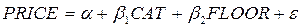 .
.
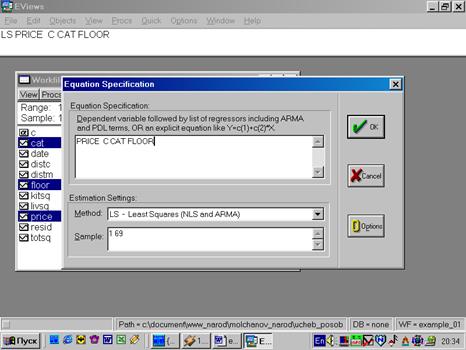
Рис. 71.
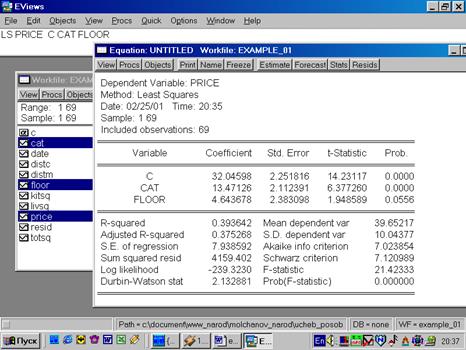
Рис. 72.
Используя результаты оценивания уравнения, содержащиеся в форме вывода (рис. 72), можно записать такое уравнение:
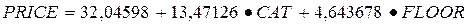 .
.
Как же можно интерпретировать полученные результаты? Полученный коэффициент при CAT означает, что квартиры в кирпичных домах стоят в среднем на $13471 дороже аналогичных квартир в панельных домах. Коэффициент при FLOOR может быть интерпретирован так: квартиры на не первом/последнем этажах стоят в среднем на $4644 дороже аналогичных, расположенных на первом/последнем этажах.
| СОДЕРЖАНИЕ | ||
| 1. | Предисловие | |
| 2. | Практическое занятие № 1. «Знакомство с эконометрическим пакетом Eviews» | |
| 3. | Практическое занятие № 2. «Применение Eviews при построении и анализе линейной однофакторной модели регрессии» | |
| 4. | Практическое занятие № 3. «Применение Eviews при построении и анализе линейной однофакторной модели регрессии» | |
| 5. | Практическое занятие № 4. «Применение Eviews при построении и анализе многофакторной модели регрессии. Выявление мультиколлинеарности и гетероскедастичности в модели. Проверка спецификации модели» | |
| 6. | Практическое занятие № 5. «Фиктивные переменные» | |
| 7. | Практическое занятие № 6. «Однофакторные стохастические модели динамических процессов» | |
КОМПЬЮТЕРНЫЙ ПРАКТИКУМ ПО НАЧАЛЬНОМУ КУРСУ ЭКОНОМЕТРИКИ (РЕАЛИЗАЦИЯ НА EVIEWS)
Дата добавления: 2015-08-11; просмотров: 926;
