Теорема о разложении вектора по базису.
Теорема. Любой вектор ЛП разлагается, причем единственным образом, в ЛК базисных векторов этого пространства.
Док-во: Рассмотрим ЛП размерности n с базисом l1, l2, ... ,ln. Вектор а Є ЛП. Система векторов l1, l2, ... ,ln, а содержит (n+1) вектор, а пространство размерности n. Отсюда следует, что система ЛЗ, т.е. линейная комбинация
α1 l1+ α2 l2+ ... +αn ln+αn+1a = 0, причем среди коэффициентов есть ≠ 0.
Покажем, что коэффициент αn+1 ≠ 0 от противного. Допустим, что αn+1 = 0. Тогда α1 l1+ α2 l2+ ... +αn ln+0 a = 0.
Отсюда следует, что α1 l1+ α2 l2+ ... +αn ln = 0 и есть ≠ 0 коэффициент.
Получили противоречие тому, что базис l1, l2, ... ,ln – ЛНЗ.
Отсюда следует αn+1 ≠ 0.
Следовательно, мы доказали, что коэффициент αn+1 ≠ 0.
Разделим на коэффициент αn+1:
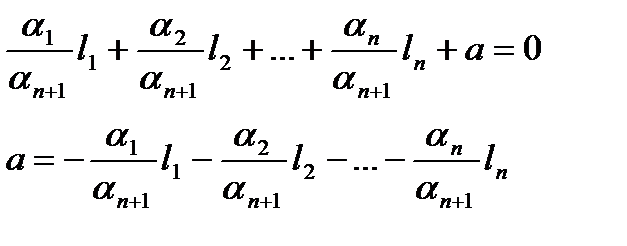
Отсюда следует, что вектор а - ЛК базисных векторов.
Докажем единственность разложения базиса от противного.
Пусть есть два разложения вектора а по базису.
a = α1 l1+ α2 l2+ ... +αn ln
a = β 1 l1+ β 2 l2+ ... + β n ln
0 = (α1- β1) l1+ (α2- β2) l2+ … + (αn- βn) ln.
Т.к. базис - ЛНЗ, то коэффициенты α1- β1=0, α2- β2=0, αn- βn=0.
Отсюда следует α1=β1, α2=β2 , αn=βn, т.е. коэффициенты совпали. Единственность разложения доказана.
Ч.т.д.
Дата добавления: 2015-08-11; просмотров: 3161;
