Координаты точки, радиус- вектор точки, произвольные вектора. Длина вектора.
Возьмем в пространстве произвольную точку М(х, у, z). Первая координата х – абсцисса ‒ это проекция т. М на ось ОХ. Вторая у – ордината – это проекция т. М на ось ОУ. Третья z – аппликата – на ось OZ.
| М |
| α |
| N |
Проекция т. М на α
Чтобы найти проекцию точки на прямую, нужно через точку провести плоскость перпендикулярно этой прямой.
| p |
| х |
| z |
| у |
| О |
| М (х, у, z) |
Определение: Вектор, соединяющий начало координат т. О с произвольной точкой пространства называется радиус- вектор этой точки.
Радиус- вектор т. М – ОМ.
Найдем координаты радиус-вектора ОМ:
ОА= xi, ОВ= yj, ОС= zk.
OM= OP+ PM= OA+ OB+ OC= xi+ yj+ zk= (x, y, z).
Вывод: координаты радиус-вектора точки совпадают с координатами самой точки ОМ= (x, y, z).
Вектор ОМ является диагональю параллелепипеда, по свойству диагоналей d2= a2+ b2+ c2 . Отсюда следует, что │ОМ│2= x2+ y2+ z2. Извлекая, квадратный корень получаем длину 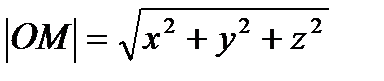 .
.
Возьмем две произвольные точки т. А(x1, y1, z1) и т. В (x2, y2, z2). Соединим АВ.
| B |
| А |
| z |
| х |
| y |
| O |
Вспомогательные векторы: ОА= (x1, y1, z1), ОВ= (x2, y2, z2).
АВ= ОВ - ОА= (x2, y2, z2)- (x1, y1, z1)= (x2- x1, , y2- y1, z2- z1).
Вывод: чтобы найти координаты вектора нужно из координат конца вектора вычесть соответствующие координаты начала вектора.
АВ= (x2- x1, , y2- y1, z2- z1).
Пример. Даны 3 точки т. А(2,-1,3), т. В(4,0,1), т. С(-1,2,1). Найти АВ и его длину │АВ│, m= AB- 2BC.
Дата добавления: 2015-08-11; просмотров: 1100;
