Приведение сил инерции твердого тела
1.Поступательное движение.Все точки тела движутся с одинаковыми траекториями и ускорениями, равными ускорению центра масс 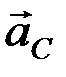 (по определению поступательного движения). Тогда имеем равнодействующую сил инерции, проходящую через центр масс:
(по определению поступательного движения). Тогда имеем равнодействующую сил инерции, проходящую через центр масс:
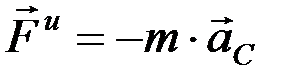 .
.
2. Вращательное движение.Пусть твердое тело вращается вокруг оси Оz, перпендикулярной плоскости хОу (плоскости материальной симметрии). Если привести силы инерции к центру О, то образуется равнодействующая сил инерции 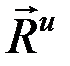 , приложенная в точке О, и главный момент сил инерции
, приложенная в точке О, и главный момент сил инерции 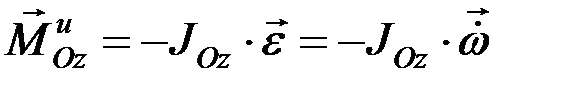 , лежащий в плоскости хОу.
, лежащий в плоскости хОу.
3. Вращение вокруг оси, проходящей через центр масс тела.В этом случае 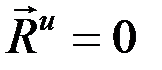 , т.к. аС = 0. Таким образом, система сил инерции тела приводится только к паре с моментом:
, т.к. аС = 0. Таким образом, система сил инерции тела приводится только к паре с моментом:
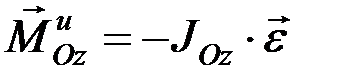 .
.
4. Плоскопараллельное движение.Если тело движется параллельно плоскости симметрии, то система сил инерции приводится к 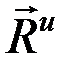 , приложенной в центре масс и паре с моментом
, приложенной в центре масс и паре с моментом
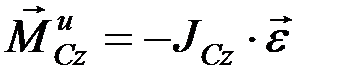 .
.
Пример.Два груза весом 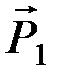 и
и  , связанные нитью, движутся по горизонтальной плоскости под действием силы
, связанные нитью, движутся по горизонтальной плоскости под действием силы  , приложенной к первому грузу. Коэффициент трения скольжения грузов о плоскость равен f. Определить ускорение грузов и натяжение нитей.
, приложенной к первому грузу. Коэффициент трения скольжения грузов о плоскость равен f. Определить ускорение грузов и натяжение нитей.
Решение.
Обозначим все действующие внешние силы и приложим в центре масс каждого из грузов силы инерции, численно равные:
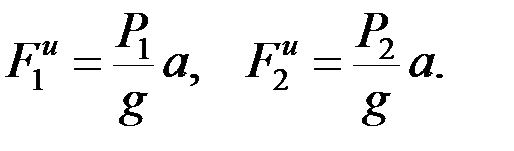
Запишем уравнение равновесия в проекции на горизонтальную ось:
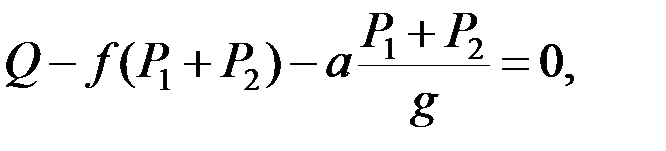
откуда
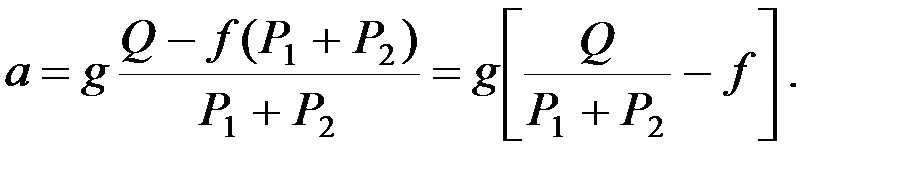

Для определения натяжения нити рассмотрим сумму проекций на горизонтальную ось всех внешних сил, действующих, например, на второй груз:

oткуда 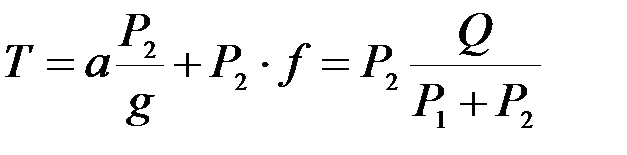 .
.
Интересно, что сила натяжения не зависит от коэффициента трения (от силы трения) и тем меньше, чем меньше вес второго груза.
Пример. На барабан весом Р и радиусом r намотана нить с грузом на конце весом  . Пренебрегая весом нити, определить угловое ускорение барабана и натяжение нити, если радиус инерции относительно оси О равен r и на барабан действует постоянный момент сил трения Мтр.
. Пренебрегая весом нити, определить угловое ускорение барабана и натяжение нити, если радиус инерции относительно оси О равен r и на барабан действует постоянный момент сил трения Мтр.
Решение.
«Остановим» груз силой инерции (т.к. он движется поступательно), а барабан – моментом сил инерции:

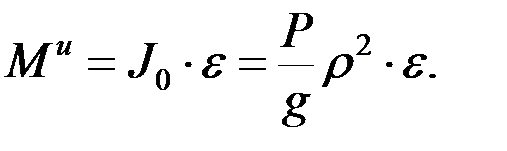
Теперь система находится в равновесии. Применим к ней уравнения статики (на рисунке не показаны вес барабана и реакция шарнира, т.к. они не дают момент относительно центра О):
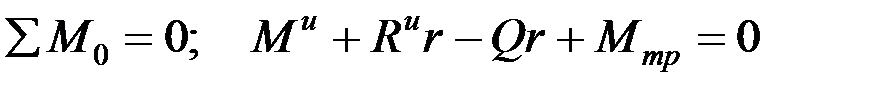
или
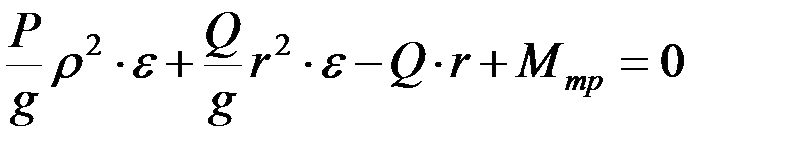 ,
,
откуда
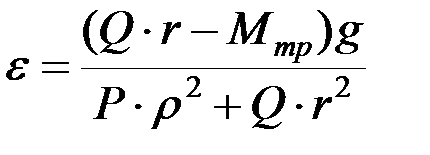 .
.
Натяжение нити определяется аналогично предыдущей задаче.
Дата добавления: 2015-08-08; просмотров: 958;
