Теорема об изменении кинетической энергии системы
Вспомним, что эта теорема для точки записывается в следующем виде:
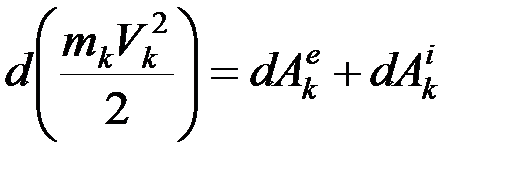 .
.
Составим также уравнения для системы из n точек и почленно их сложим:
 или
или 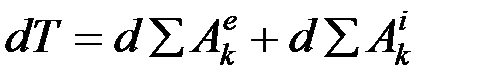 .
.
Это равенство выражает теорему об изменении кинетической энергии системы в дифференциальной форме. Интегрируя, получим запись теоремы в интегральной форме:
 .
.
Изменение кинетической энергии системы при некотором ее перемещении равно сумме работ на этом перемещении всех приложенных к системе внешних и внутренних сил.
 В отличие от других теорем внутренние силы здесь не исключаются. Несмотря на то, что
В отличие от других теорем внутренние силы здесь не исключаются. Несмотря на то, что 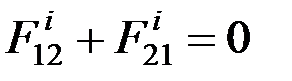 , точки B1 и B2 могут перемещаться по направлению друг к другу, а работы сил будут положительными и сумма работа не равна нулю.
, точки B1 и B2 могут перемещаться по направлению друг к другу, а работы сил будут положительными и сумма работа не равна нулю.
Неизменяемой называется такая система, в которой расстояние между каждыми двумя точками в течение всего времени движения остается неизменным.
По теореме о проекциях скоростей,
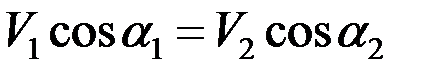
или, поскольку  ,
,
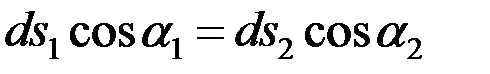 .
.
Кроме того, 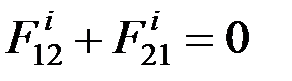 , тогда
, тогда
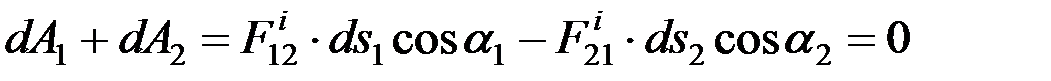 .
.
В случае неизменяемой системы сумма работ внутренних сил равна нулю, а уравнение теоремы об изменении кинетической энергии в дифференциальной форме примет вид:
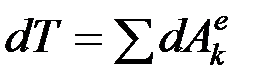 ,
,
откуда путем интегрирования получим:
 .
.
Изменение кинетической энергии неизменяемой системы при некотором ее перемещении равно сумме работ на этом перемещении всех приложенных к системе внешних сил.
Дата добавления: 2015-08-08; просмотров: 811;
