Скорость точки при координатном задании движения.
Координаты точки М одновременно являются и координатами её радиус-вектора. Поэтому координатное задание движения точки эквивалентно заданию движения её векторным способом. Разложим вектор скорости точки и её радиус-вектор в направлении координатных осей:
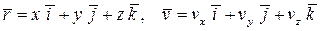 .
.
Согласно определению, данному выше, вектор скорости равен производной от радиус-вектора движущейся точки по времени
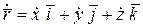 .
.
Сравнивая эту формулу с предыдущими соотношениями, убеждаемся, что проекция скорости на какую-либо ось равна производной от соответствующей координаты по времени
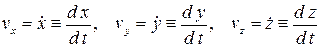
В силу ортогональности составляющих вектора скорости, легко определить её модуль и направляющие косинусы
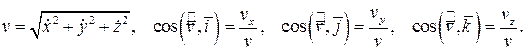
Дата добавления: 2015-08-08; просмотров: 671;
