Аксиомы статики
Условия, при которых тело может находиться в равновесии, выводиться из нескольких основных положений, применяемых без доказательств, но подтвержденных опытом и называемых аксиомами статики. Основные аксиомы статики сформулированы выдающимся английским ученым Исааком Ньютоном и поэтому названы его именем.
Аксиома I(аксиома инерции, или первый закон Ньютона). Всякое тело сохраняет свое состояние покоя или прямолинейного равномерного движения до тех пор, пока какие – нибудь силы не выведут тело из этого состояния.
Способность материального тела сохранять движение при отсутствии действующих сил или постепенно изменять это движение, когда на тело начинают действовать силы, называется инерцией или инертностью. Инертность есть одно из основных свойств материи.
В соответствии с этой аксиомой состоянием равновесия считается такое состояние, когда тело находиться в покое или движется прямолинейно и равномерно, т.е. по инерции.
Аксиома II(аксиома взаимодействия, или третий закон Ньютона). Силы взаимодействия двух тел всегда равны по модулю ( |F1| = |F2| или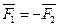 
)и направлены по одной прямой и в противоположные стороны.
Рис. 1.2 Из третьего закона Ньютона вытекает, что одностороннего механического действия одного тела на другое не существует, т.е. силы взаимодействия – силы парные. Однако сила действия одного тела на другое и сила противодействия не представляет собой систему сил, т.к. они приложены к разным телам.
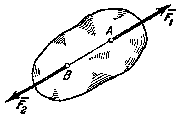
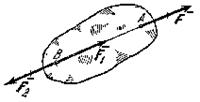
Аксиома III(закон равенства действия и противодействия). Для равновесия свободного твердого тела, находящегося под действием двух сил, необходимо и достаточно, чтобы эти силы были равны по модулю и действовали по одной прямой в противоположные стороны.
Закон о равенстве действия и противодействия является одним из основных законов механики. Из него следует, что если тело А действует на тело В с силой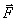 
, то одновременно тело В действует на тело А с такой же по модулю и направленной вдоль той же прямой, но противоположную сторону силой 
= 
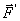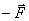(рис. 1.3). Однако силы 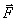и 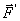не образуют уравновешенной системы сил, так как они приложены к разным телам.
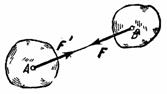рис. 1.3.
Аксиома IV(принцип присоединения и отбрасывания систем сил, эквивалентной нулю). Всякую силу, действующую на абсолютно твердое тело, можно перенести вдоль линии ее действия в любую точку, не нарушив при этом его механического состояния.
Следствие из 2-й и 4-й аксиом. Действие силы на абсолютно твердое тело не изменится, если перенести точку приложения силы вдоль ее линии действия в любую другую точку тела.
В самом деле, пусть на твердое тело действует приложенная в точке А сила 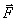(рис. 1.4). Возьмем на линии действия этой силы произвольную точку В и приложим к ней две уравновешенные силы 
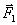и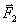 
, такие, что 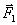= 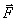, 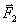= 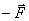. От этого действие силы 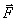на тело не изменится.
Но силы 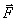и 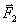согласно аксиоме 2 рис. 1.4.
также образуют уравновешенную систему, которая может быть отброшена. В результате на тело будет действовать только одна сила 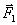, равная , но приложенная в точке В.
Таким образом, вектор, изображающий силу , можно считать приложенным в любой точке на линии действия силы (такой вектор называется скользящим).
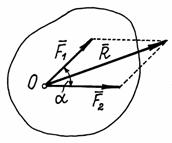
Аксиома V(правило параллелограмма). Равнодействующая двух сил, приложенных к телу в одной точке, приложена в той же точке, равна по модулю и совпадает по направлению с диагональю параллелограмма, построенного на данных силах.
Вектор 
, равный диагонали параллелограмма, построенного на векторах 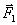и 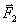(рис.12), называется геометрической суммой векторов 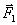и : = + .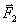
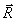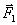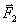Величина равнодействующей
Рис. 1.3.
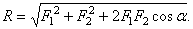
Конечно,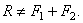 
Такое равенство будет соблюдаться только при условии, что эти силы направлены по одной прямой в одну сторону. Если же векторы сил окажутся перпендикулярными, рис. 1.5
то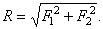 
Следовательно, аксиому 3 можно еще формулировать так: две силы, приложенные к телу в одной точке, имеют равнодействующую, равную геометрической (векторной) сумме этих сил и приложенную в той же точке.
Аксиома 5 (принцип отвердевания). Равновесие изменяемого (деформируемого) тела, находящегося под действием данной системы сил, не нарушится, если тело считать отвердевшим (абсолютно твердым).
Высказанное в этой аксиоме утверждение очевидно. Например, ясно, что равновесие цепи не нарушится, если ее звенья считать сваренными друг с другом и т. д.
Дата добавления: 2015-08-08; просмотров: 4377;