Связи и реакции связей
Все законы и теоремы статики справедливы для свободного твердого тела.
Все тела делятся на свободные и связанные.
Свободным называется тело, которое не испытывает никаких препятствий для перемещения в пространстве в любом направлении. Если же тело связано с другими телами, которые ограничивают его движение в одном или нескольких направлениях, то оно является несвободным. Тела, которые ограничивают движение рассматриваемого тела, называют связями.
При взаимодействии между телом и его связями возникают силы, противодействующие возможным движениям тела. Эти силы действуют на тело со стороны связей и называются реакциями связей.
Реакция связи всегда противоположна тому направлению, по которому связь препятствует движению тела. Существование реакцией основывается аксиомой связей используют принцип освобождения от связей. Не изменяя равновесия тела, каждую связь можно отбросить, заменяя ее реакцией. Определение реакций связей является одной из наиболее важных задач статики.
Все связи можно разделить на несколько типов.
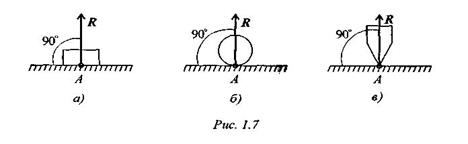
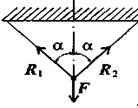
Рис. 1.6
1) Связь – гладкая опора (без трения).
Реакция опоры приложена в точке опоры и всегда направлена перпендикулярно опоре (рис. 1.7).
2) Гибкая связь (нить, веревка, трос, цепь). Груз подвешен на двух нитях (рис. 1.6). Реакция нити направлена вдоль нити от тела, при этом нить может быть только растянута.
3) Жесткий стержень. На схемах стержни изображают толстой сплошной линией (рис. 1.8).
 Стержень может быть сжат или растянут. Реакция стержня направлена вдоль стержня. Стержень работает на растяжение или сжатие. Точное направление реакции определяют, мысленно убрав стержень и рассмотрев возможные перемещения тела без этой связи.
Стержень может быть сжат или растянут. Реакция стержня направлена вдоль стержня. Стержень работает на растяжение или сжатие. Точное направление реакции определяют, мысленно убрав стержень и рассмотрев возможные перемещения тела без этой связи.
Возможным перемещением точки называется такое бесконечно малое мысленное перемещение, которое допускается в данный момент наложенными на него связями.
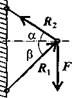
 Убираем стержень 1, в этом случае стержень 2 падает вниз. Следовательно, сила от стержня 1 (реакция) направлена вверх. Убираем стержень 2. В этом случае точка А
Убираем стержень 1, в этом случае стержень 2 падает вниз. Следовательно, сила от стержня 1 (реакция) направлена вверх. Убираем стержень 2. В этом случае точка А
рис 1.8 опускается вниз, отодвигаясь от стены. Следовательно, реакция стержня 2 направлена к стене.
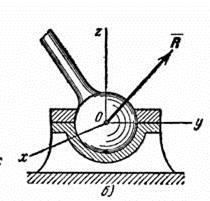
 4) Сферический шарнир.Этот вид вид связи закрепляет тело таким образом, что оно не может
4) Сферический шарнир.Этот вид вид связи закрепляет тело таким образом, что оно не может
Рис. 1.9
совершать никаких поступательных перемещений в пространстве, а может только поворачивается относительно трех координатных осей, проходящих через центр шарнира. Для нахождения модуля и направления реакции R ее необходимо заменить тремя составляющими x, y, z с линями действия, параллельными осями координат.
Рис. 1.10
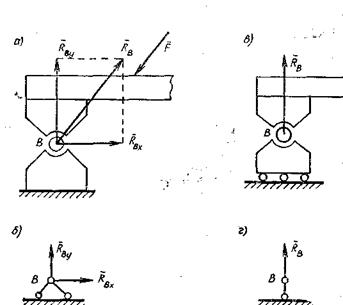
5) Шарнирно – неподвижная опора.(рис. 1.10,а). Эта опора препятствует любому поступательному перемещению системы в ее плоскости, но дает ей возможность свободно поворачиваться вокруг оси шарнира (трением в шарнире пренебрегаем). Схематически такая опора изображается двумя стержнями (рис. 1.10, б), шарнирно соединенными на одном конце. Реакция такой опоры проходит через ось шарнира, но неизвестна как по модулю, так и по направлению и, следовательно, характеризуется двумя неизвестными величинами. Для их нахождения реакцию Rв необходимо заменить двумя взаимно перпендикулярными составляющими RВх и RВу,.
6)Шарнирно-подвижная опора(рис. 1.10,в). Эта опора препятствует лишь перемещению, перпендикулярному к опорной плоскости, но не препятствует перемещению оси шарнира параллельно этой плоскости. Реакция шарнирно-подвижной опоры всегда перпендикулярна опорной плоскости. Таким образом, для шарнирно-подвижной опоры неизвестна только величина реакции. Схематически такая опора изображается в виде одного стержня с шарнирами по концам (рис. 1.10, г). Реакция такой опоры проходит через ось шарнира и направлена вдоль стержня.
 Шарнирно – неподвижная и шарнирно – подвижная опоры являются опорами балочных систем.
Шарнирно – неподвижная и шарнирно – подвижная опоры являются опорами балочных систем.
7)Защемление или «заделка». Любые перемещения точки крепления не возможны.
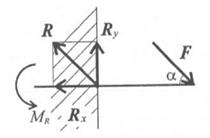
Под действием внешних сил в опоре возникают реактивная сила и реактивный момент Mr, препятствующий повороту (рис. 1.11).
Реактивную силу принято представлять в виде двух составляющих вдоль осей координат R = Rx + Ry.
рис. 1.11
Дата добавления: 2015-08-08; просмотров: 2728;
