ЭЛЕМЕНТЫ КВАНТОВОЙ СТАТИСТИКИ И ФИЗИКИ ТВЕРДОГО ТЕЛА. 10.Теория Дебая. Теплоемкость кристаллической решетки.

(продолжение)

ТЕПЛОВЫЕ СВОЙСТВА ТВЕРДЫХ ТЕЛ.

8. Закон Дюлонга – Пти.

9.Теория Эйнштейна.

10.Теория Дебая. Теплоемкость кристаллической решетки.

11. Теплоемкость электронного газа в металлах.

Тепловое движение частиц в твердых телах представляет малые хаотические колебания атомов и молекул около положения равновесия; а также случайные переходы атомов из одного квантового состояния в другое. Наиболее часто такие переходы совершают свободные электроны в металлах.

С ростом температуры увеличивается амплитуда колебаний атомов, а свободные электроны в металле переходят на более высокие энергетические уровни. Все это приводит к увеличению внутренней энергии кристалла.

Можно сделать вывод, что зависимость внутренней энергии кристалла определяется температурными зависимостями энергии кристаллической решетки 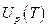и внутренней энергии электронного газа :

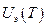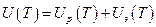
Тогда молярную теплоемкость кристалла можно представить как сумму молярных теплоемкостей кристаллической решетки и электронного газа:

.

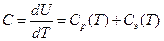В неметаллических телах почти нет свободных электронов, поэтому их теплоемкость определяется только теплоемкостью кристаллической решетки.

Будем считать колеблющейся атом гармоническим осциллятором, энергия которого равна:

,

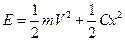где C – const, определяющая свойства атомов.

По классическим представлениям на одну степень свободы атома приходится средняя энергия, равная 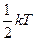, где k – постоянная Больцмана.

, поэтому общее значение энергии, приходящееся на одну степень свободы и состоящей из двух слагаемых, равно kT.

Атом может колебаться в трех взаимно перпендикулярных направлениях, следовательно, его энергия равна .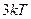

Твердое тело, состоящее из N атомов, будет иметь энергию равную:

.

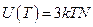И тогда теплоемкость кристаллической решетки можно выразить:

.

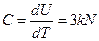Если рассматривать один моль вещества, то 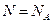, и учитывая, что 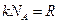, получим, что молярная теплоемкость будет равна:

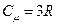
Этот закон был получен экспериментально французскими физиками Дюлонгом и Пти, но

справедлив он только при достаточно высоких температурах, превышающих некоторое значение 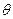, называемое температурой Дебая, которая для различных веществ может принимать значения от 200 К до 2000 К.

Эксперимент показал, что при температурах ниже дебаевской, молярная теплоемкость кристаллов пропорциональна .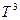

По классическим представлениям кристалл, состоящий из N атомов, является системой с 3N колебательными степенями свободы, на каждую из которых приходится в среднем энергия kT . Из этих представлений вытекает закон Дюлонга-Пти, который утверждает, что молярная теплоемкость всех химически простых веществ в кристаллическом состоянии равна 3R. Как уже отмечалось, этот закон справедлив только при сравнительно высоких температурах. При низких температурах теплоемкость кристаллов убывает, стремясь к нулю при T 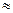0 К.

В 1907 году Эйнштейн создал теорию теплоемкости кристаллов, в которой учел, что энергия гармонического осциллятора квантуется:

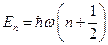
Предположив, что распределение осцилляторов по состояниям с различной энергией подчиняется распределению Больцмана, он получил для него среднее значение энергии.

,

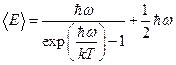где 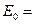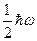- энергия нулевых колебаний осциллятора.

Если предположить, что все атомы в кристалле колеблются с одинаковой частотой, то его внутренняя энергия будет равна:

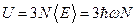
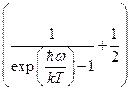
Учитывая, что 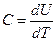, получим при низких температурах:

.

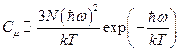Это выражение обращается в ноль при Т 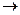0К. Однако оно не согласуется 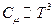, т.е. дает только качественное совпадение с экспериментально установленной зависимостью.

Количественного согласия с экспериментом удалось добиться Дебаю в 1912 году. По Дебаю кристалл представляет собой систему из N упруго связанных гармонических осцилляторов, обладающих 3N степенями свободы. Колебания такой системы имеют характер стоячих волн с дискретными частотами 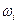, т.е. в кристалле существует 3N типов простейших независимых колебаний, называемых нормальными колебаниями или модами.

Энергия одного нормального колебания может иметь значения:

.

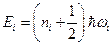
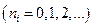Энергию кристалла можно представить как сумму нормальных колебаний:

,

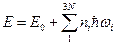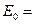
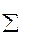
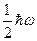
где 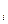- энергия нулевых колебаний осцилляторов.

Если вычесть энергию нулевых колебаний, то получается, что энергия нормальных колебаний складывается из порций 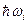, которые можно назвать квантами звука. Это дает возможность сопоставить нормальному колебанию квазичастицу называемую фонон.