Фонон – не частица в прямом смысле, это возбужденное состояние, распределенное по всему объёму кристалла.

Многие процессы в кристалле протекают так, как если бы фонон обладал импульсом равным:

,

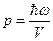где V – скорость упругих волн в кристалле.

Однако в отличии от обычных частиц, фонон не может возникнуть в вакууме. Для его существования нужна среда.

Кроме того, при взаимодействии фононов друг с другом, их импульс меняется дискретными порциями и может передаваться кристаллической решетке. Получается, что импульс фонона не подчиняется закону сохранения импульса, поэтому его называют квазиимпульсом. Одновременно в кристалле может возбуждаться неограниченное число фононов, следовательно, принцип запрета Паули на них не распространяется.

Таким образом, колебания кристаллической решетки можно представить как фононный газ, заключенный в пределах кристалла, подобно тому, как электромагнитное излучение можно представить как фотонный газ.

Это сходство чисто формальное и хотя фотоны и фононы подчиняются одной статистике, фотоны – это истинные частицы, а фононы – квазичастицы.

Применив к фононному газу распределение Бозе-Эйнштейна

,

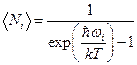Дебай получил для теплоемкости кристаллической решетки следующее выражение:

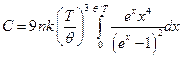
где .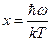

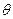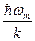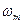Характеристическая температура Дебая равна: = , где - максимальная частота нормальных колебаний равная: 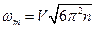, где V – скорость упругих волн в кристалле, n – концентрация атомов в кристалле.

При 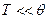верхний предел интегрирования будет очень большой и его можно приравнять к 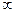. Тогда можно считать, что 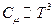, и для одного моля в этом случае

,

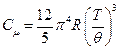где R – универсальная газовая постоянная.

Закон Дебая хорошо выполняется при низких температурах в кристаллах с простой кристаллической решеткой. К кристаллам со сложной структурой формула Дебая неприменима. При 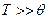- этот закон переходит в закон Дюлонга-Пти.

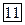По классическим представлениям электронный газ должен обладать молярной теплоемкостью, равной 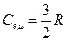. Согласно закону Дюлонга-Пти молярная теплоемкость решетки составляет 3R. Следовательно, теплоемкость металлов должно в полтора раза превышать теплоемкость диэлектриков. В действительности теплоемкость металлов не отличается существенно от теплоемкости неметаллических кристаллов. Это противоречие устраняется квантовой теорией теплоемкости.

Средняя энергия теплового движения, равная по порядку величине kT, составляет при комнатной температуре примерно 0,025 эВ. Такая энергия может возбудить только электроны, находящиеся на самых верхних уровнях, примыкающих к уровню Ферми. Основная масса электронов, размещенных на более глубоких уровнях, остается в прежних состояниях и поглощать энергию при нагревании не будет. Таким образом, в процессе нагревания металла участвует незначительная часть электронов проводимости, чем и объясняется малая теплоемкость электронного газа в металлах.

Внутренняя энергия свободных электронов в металле при Т = 0 К составляет величину, определяемую соотношением:

.

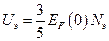
При не очень высоких температурах расчет приводит к зависимости внутренней энергии электронного газа от температуры, определяемой соотношением:

.

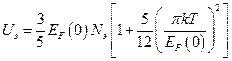В случае, если температура кристалла значительно выше температуры Ферми и электронный газ становится невырожденным его внутренняя энергия равна:

.

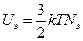По определению теплоемкость определяется производной .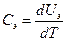

В результате получим, что при низких температурах:

,

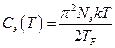и при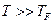

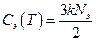
Теплоемкость металлов складывается из теплоемкости кристаллической решетки и теплоемкости электронного газа:

,

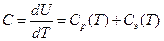температурные зависимости которых характеризуются температурой Дебая и температурой Ферми. Для металлов температура Ферми, как уже отмечалось, составляет величину порядка 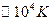, т.е. температура Дебая оказывается существенно ниже температуры Ферми. Это приводит к тому, что при низких температурах 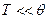теплоемкость электронного газа выше теплоемкости кристаллической решетки. С повышением температуры теплоемкость решетки быстро растет и становится больше теплоемкости электронного газа. Это справедливо в силу того, что электронный газ остается вырожденным.

ЛЕКЦИЯ 12

ФИЗИКА АТОМНОГО ЯДРА.

1. Состав и характеристики атомного ядра.

2. Дефект массы и энергия связи атомного ядра.

3. Ядерное взаимодействие.

4. Радиоактивность. Закон радиоактивного распада.

По современным представлениям ядро атома состоит из элементарных частиц -нуклонов, которые бывают двух типов: протоны и нейтроны.

Протоны – положительно заряженные частицы, заряд которых по модулю равен заряду электрона 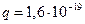Кл, и масса которых в свободном состоянии составляет 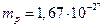кг 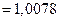а.е.м.

Количество протонов в ядре называют зарядовым числом, обозначают Z. Определяется оно порядковым номером элемента в таблице Менделеева.

Нейтроны – электронейтральные частицы ( 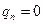), масса которых в свободном состоянии равна 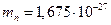кг 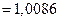а.е.м.

Общее количество нуклонов в ядре называют массовым числом и обозначают А. Оно равно массе элемента, указанной в таблице Менделеева, округленной до целого числа.

Тогда количество нейтронов в ядре равно:

.

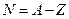Протон и нейтрон обладают полуцелым спином 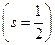и собственным магнитным моментом, несмотря на то, что у нейтрона нет электрического заряда.

Магнитный момент протона равен: ,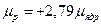

магнитный момент нейтрона - ,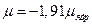

где 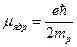= 5,05 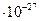Дж/Тл – ядерный магнетон.

Знак 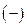у собственного магнитного момента нейтрона означает, что направления собственных механического и магнитного моментов противоположны.

В свободном состоянии нейтрон является нестабильным образованием и подвержен радиоактивному распаду.

Ядра различных химических элементов обозначают символом соответствующего элемента из таблицы Менделеева. Слева сверху ставиться массовое число, снизу указывается зарядовое число:

.

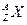В ядрах одного и того же химического элемента число протонов всегда одинаково, а число нейтронов может быть различным.