ЭЛЕМЕНТЫ КВАНТОВОЙ СТАТИСТИКИ И ФИЗИКИ ТВЕРДОГО ТЕЛА

ЭЛЕКТРИЧЕСКИЕ СВОЙСТВА ТВЕРДЫХ ТЕЛ

1. Электроны в кристаллах.

2. Зонная теория электронных спектров.

3. Распределение электронов по состояниям. Функция Ферми-Дирака.

4. Металлы, проводимость металлов. Диэлектрики и полупроводники.

Твердое тело есть агрегатное состояние вещества, находясь в котором оно сохраняет свою форму. Микроскопическая структура твердого тела может быть кристаллической или аморфной. В кристаллах атомы расположены регулярными рядами и образуют так называемую кристаллическую решетку. Положения равновесия, около которых совершают колебания атомы, называются узлами кристаллической решетки.

Каждый атом, как известно, состоит из положительного ядра и нескольких отрицательных электронов, которые вращаются около ядра. Масса электрона существенно меньше массы ядра любого атома, поэтому в твердых телах электроны обладают большей подвижностью, чем ядра.

Для понимания физических процессов, определяющих электрические и тепловые свойства, примем следующую модель твердого тела.

Будем считать, что ядра атомов неподвижны, а электроны двигаются в пространстве между ними. Так как электроны являются микрочастицами, то для описания их движения в кристаллической решетке будем применять методы и законы квантовой механики.

Будем описывать движение одного электрона волновой функцией 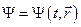, которая является решением уравнения Шрёдингера:

,

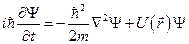где m- масса электрона; 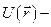потенциальная энергия электрона, определяемая его взаимодействием с ядром и другими электронами; 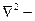оператор Лапласа.

Физический смысл волновой функции в данном случае заключается в том, что выражение:

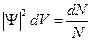
есть вероятность обнаружить рассматриваемый электрон в объёме dV. Интегрирование этого соотношения по всему объёму в котором движутся электроны (объём кристалла) приводит к условию нормировки:

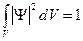
Что бы определить конкретный вид волновой функции 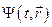необходимо знать закон изменения потенциальной энергии электрона в объёме кристалла. Эта энергия складывается из энергии взаимодействия данного электрона с ядром 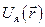и энергии взаимодействия его с другими электронами .

+ .

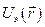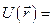
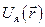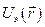Энергия взаимодействия электрона с одним из ядер кристаллической решетки будет равна: ,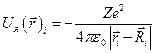

где 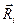- радиус-вектор, определяющий положение ядра, 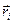- радиус-вектор, определяющий положение электрона.

Поскольку кристаллическая решетка это совокупность атомных ядер, то общую энергию взаимодействия электрона со всей кристаллической решеткой можно записать:

.

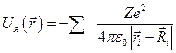Потенциальная энергия взаимодействия одного электрона со всеми другими электронами 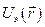описывается более сложной функцией и поэтому строгое решение уравнения Шрёдингера для электрона в кристаллической решетке представляет собой сложную математическую задачу. Однако это уравнение имеет простое приближенное решение, которое можно получить на основе следующих соображений.

Каждый атом можно считать по отношению к рассматриваемому электрону электронейтральным, т.к. электрон, двигаясь в пространстве кристаллической решетки с большой скоростью «не успевает разглядеть остальные электроны» и тогда его потенциальная энергия будет равна нулю 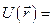0. Такой электрон можно считать свободным.

Если же электрон движется внутри атома около ядра, то именно взаимодействие с ядром определяет характер его движения. Электроны, наиболее удаленные от ядра, называются внешними или валентными и они слабее связаны с атомов, чем внутренние. Даже небольшое внешнее воздействие способно оторвать такой электрон от ядра, и он станет свободным.Приближение, в котором пренебрегают воздействием ядер и электронов на движение отдельного электрона, называется «приближением свободных электронов».

Свободные электроны в металле ведут себя подобно молекулам идеального газа. Поэтому их называют электронным газом. Ранее мы выяснили, что энергия частицы, находящейся в потенциальной яме квантуется. Металлический образец представляет собой для электронов трехмерную потенциальную яму. Решение уравнения Шрёдингера для такой частицы показало, что энергия их может принимать только дискретные (квантованные) значения.

Уравнение Шрёдингера для приближения свободных электронов приобретает вид:

.

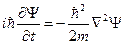И движение свободного электрона описывается волновой функцией вида:

,

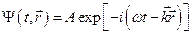которая представляет собой плоскую волну. При этом волновой вектор 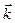и частота 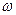волны связаны с импульсом электрона 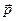и сего энергией соотношениями де Бройля:

.

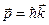
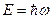Надо помнить, что «приближение свободных электронов»справедливо только для внешних электронов, для внутренних электронов оно неприменимо.

Состояние электрона в кристалле описывается волновой функцией:

,

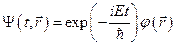где 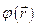- решение стационарного уравнения Шрёдингера:

.

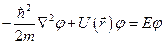Решив это уравнение, можно найти спектр энергий электрона и набор соответствующих волновых функций, описывающих поведение электрона в кристалле.

Вследствие взаимодействия электронов одного атома с ядрами и электронами других атомов в кристаллической решетке спектр энергий кристалла должен отличаться от спектра энергий отдельного атома. В то же время должно существовать и некоторое соответствие между этими спектрами.

Вместо одного энергетического уровня в спектре энергий электрона, находящегося в кристалле из N одинаковых атомов, имеются N очень близко расположенных уровней. Совокупность таких уровней называется энергетической зоной.

Интервалы энергий, которые не может иметь электрон, образуют запрещенные зоны.

Рис.31

Энергетические зоны в кристалле.

Чтобы понять происхождение зон, рассмотрим воображаемый процесс объединение атомов в кристалл.

Пусть первоначально имеется N изолированных атомов какого-либо вещества. Пока атомы изолированы, схемы их энергетических уровней полностью совпадают. По мере сближения атомов между ними возникает усиливающееся взаимодействие, которое приводит к изменению положений уровней. Вместо одного одинакового для всех атомов уровня возникают N очень близких, но не совпадающих уровней. То есть, каждый уровень

изолированного атома расщепляется в кристалле на густо расположенные уровни, образующие зону.

Таким образом, спектр энергий электронов в кристалле представляет собой бесконечную последовательность энергетических разрешенных зон, разделенных запрещенными зонами, Рис 31.

Взаимодействие с соседними атомами сильнее всего сказываются на внешних (валентных) электронах, поэтому уровни этих электронов образуют наиболее широкую зону, которая называется валентной. Электроны, оторвавшиеся от своих атомов и ставшие свободными, располагаются на уровнях с большей энергией, чем валентные электроны. Эти уровни образуют следующую зону, названную зоной проводимости или свободной зоной.

В зависимости от свойств атома между разрешенными зонами, возникшими из соседних уровней атома, может находиться запрещенная зона или происходит перекрывание зон.

Число уровней в такой слившейся зоне равно сумме количества уровней, на которые расщепляются оба первоначальных уровня. Ширина зон не зависит от размера кристалла. Это значит, что чем больше атомов в кристалле, тем теснее располагаются уровни в зоне.

Разность между 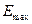(значение энергии, соответствующее самому верхнему уровню) и 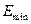(значение энергии, соответствующее самому нижнему уровню в зоне) называется шириной зоны .

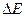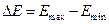
Разность между «потолком» валентной зоны и «дном» зоны проводимости называют шириной запрещенной зоны.

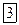В любой равновесной системе частицы распределяются так, что внутренняя энергия системы принимает минимальное значение.

При абсолютном нуле электроны в кристалле располагаются попарно на самых нижних доступных для них энергетических уровнях.

Это приводит к тому, что при T = 0 К все энергетические состояния с энергией от наименьшей 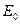до состояния с энергией 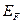заняты электронами (по одному в каждом состоянии), а все состояния с энергией большей, чем 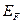свободны.

Распределение электронов по энергетическим состояниям в кристалле подчиняется принципу Паули, согласно которому в одном состоянии, характеризуемом четырьмя квантовыми числами, не может быть более одного электрона. Иначе говоря, на одном энергетическом уровне может одновременно находиться не более двух электронов с антипараллельными спинами .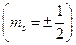

Зависимость числа электронов в одном состоянии от его энергии можно выразить соотношением:

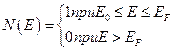
Граничное значение энергии 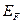называют энергией Ферми или уровнем Ферми.