При абсолютном нуле уровень Ферми совпадает с верхним заполненным электронами уровнем

,

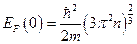где m- масса электрона, n – концентрация свободных электронов в металле, 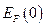- значение энергии Ферми при абсолютном нуле.

Средняя энергия одного электрона в металле при абсолютном нуле равна:

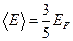(0)

Величина 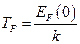называется температурой Ферми.

При температуре выше абсолютного нуля электроны совершают тепловое движение, т.е. переходят из одного состояния в другое. При этом одно какое-либо состояние не может быть все время свободно или все время занято. Электроны то уходят из него, то возвращаются обратно.

Равновесное распределение электронов по состояниям характеризуется вероятностью заполнения состояния или средним числом электронов в данном состоянии, которое описывается функцией Ферми-Дирака:

, ( )

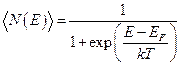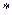где 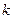- константа Больцмана.

На Рис. 32 приведен график изменения функции Ферми-Дирака (распределение электронов по состояниям) от величины энергии электронного уровня.: сплошной линией при 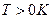и пунктир при .

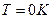Рис. 32

Из графика видно, что при 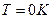вероятность заполнения уровней с 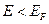равнаединице, а с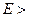 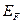равна нулю.

При 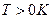значения функции Ферми-Дирака при 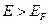уже не равны нулю, следовательно, не равна нулю и вероятность заполнения электронами этих уровней.

Значения же 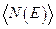, соответствующие значениям энергии 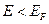меньше единицы, т.е среди этих уровней могут появиться свободные, не заполненные электронами уровни.

При 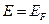функция Ферми-Дирака равна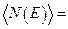 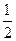, а её производная равна:

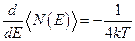
Используя эти значения, запишем уравнение касательной к графику функции Ферми-Дирака в точке :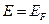

.

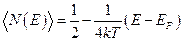Рис.33

Из графика видно, что при 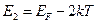функция 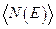становится равной единице, при 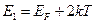пересекает ось Е, а при 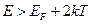стремится к нулю.

Это означает, что почти все состояния с энергиями 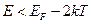заняты электронами, а состояния с энергиями 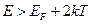свободны.

Из этого следует, что в тепловом (хаотическом) движении участвует сравнительно небольшое число электронов, энергия которых лежит в интервале от 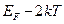до 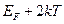. Ширина этого интервала равна .

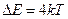Так как множество состояний электронов в кристалле является счетным , припишем каждому из них порядковый номер n = 1,2,…

Тогда формулу со ( ) можно переписать:

,

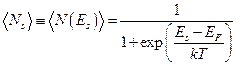где 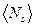- среднее число электронов в состоянии под номером s, 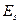- энергия электрона в этом состоянии.

Очевидно, что сумма всех 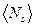равна полному числу электронов в кристалле, т.е.

.

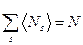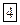а) Средняя скорость электронов в кристалле.