Уровней), между которыми происходит скачкообразный переход.

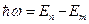
3. Орбита электрона будет стационарной, если его момент импульса на этой орбите будет кратен постоянной Планка.

,

где n = 1,2,3,… 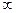называют главным квантовым числом и оно определяет номер орбиты.

Один из аргументов де Бройля в пользу волновой природы элементарных частиц состоял в том, что его предположение позволяло объяснить существование стационарных орбит электрона.

Согласно волновой теории вещества, частице массой m, движущейся со скоростью V, соответствует волна, длина которой равна:

.

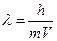Де Бройль высказал предположение, что электронам соответствуют круговые стоячие волны, которые замыкаются на себя. Если длина волны такова, что не позволяет ей замкнуться на круговой орбите, то происходит ослабляющая интерференция Рис.20а и такая волна практически мгновенно затухает Рис.20а. Если на круговой орбите укладывается целое число длин волн, то в результате интерференции образуется стоячая волна, которая, как известно, не переносит энергию, следовательно, может существовать бесконечно долго Рис 20б.

а) б)

Рис.20

То есть: .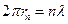

Подставив в это выражение длину волны де Бройля, получим:

,

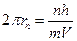или

; .

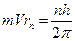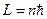А это есть не что иное, как условие квантования орбит по Бору.

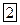Существование в атоме дискретных энергетических уровней было подтверждено опытами немецких физиков Франка и Герца в 1914 году.

Рис.21. Схема опыта Франка и Герца.

В трубке, заполненной парами ртути при небольшом давлении ( 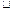1 гектопаскаля), имелись три электрода: К-катод, А-анод и С-сетка. Электроны, вылетевшие из катода вследствие термоэлектронной эмиссии, ускорялись разностью потенциалов U между катодом и сеткой. Между сеткой и анодом приложено слабое электрическое поле (0,5В), тормозившее движение электронов к аноду. Полученная на такой установке вольтамперная характеристика приведена на Рис.22.

Рис.22

Сначала сила тока монотонно возрастала, достигая максимума при U 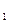= 4,9В, после чего резко падала и снова начинала расти. Максимумы повторялись при напряжениях кратных U 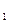, т.е. 9,8;14,7 и т.д.

Такой ход кривой можно объяснить тем, что вследствие дискретности энергетических уровней атомы могут воспринимать энергию только порциями .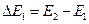

До тех пор пока энергия электрона меньше чем 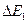, соударения между электроном и атомом ртути носят упругий характер. Часть электронов попадают на сетку, остальные продолжают движение к аноду, преодолевая тормозящее поле, и создают ток в цепи.

Когда энергия, накапливаемая электроном в промежутке катод – сетка, достигает значения 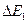, соударения перестают быть упругими, электроны отдают энергию 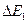атомам ртути .и сами продолжают двигаться дальше, но они уже не в состоянии преодолеть поле за сеткой, поэтому ток уменьшается. При дальнейшем росте напряжения электрон на пути катод -анод может испытать дважды неупругое соударение с атомами ртути, теряя при этом энергию 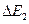, вследствие чего сила тока снова уменьшается и процесс повторится.

Таким образом, в опыте Франка и Герца непосредственно обнаруживается существование у атомов дискретных уровней.

Исходя из своих постулатов и условия квантования стационарных орбит, Бор создал полуклассическую полуквантовую теорию атома водорода.

Заряд ядра этого атома составляет 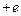, на орбите атома водорода всего один электрон. Движение этого электрона можно описать двумя уравнениями, первое из которых является уравнением, составленным по 2-ому закону Ньютона, второе – условие квантования орбит.

Центростремительное ускорение создает сила Кулона, которая удерживает электрон у ядра, следовательно:

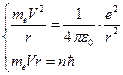, (1)

где V- скорость электрона на орбите, r- радиус орбиты, m 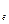- масса электрона.

Выразив из 2-го уравнения скорость электрона и подставив её в 1-ое уравнение, получим выражение для радиусов, разрешенных орбит:

.

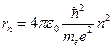При n = 1 ;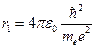

то есть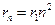

Радиус 1-ой стационарной орбиты называется боровским радиусом, который равен:

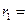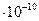0,529 м.

Внутренняя энергия атома складывается из кинетической энергии электрона (ядро считается неподвижным) и энергии взаимодействия электрона с ядром:

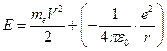, (2)

где последнее слагаемое определяет потенциальную энергию электрона в ядре, которая считается отрицательной.

Из 1-го уравнения системы (1) выразим 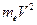и подставим его в выражение для полной энергии атома (2), в результате получим:

.

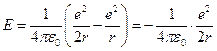Подставим в него полученное ранее выражение для 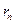, запишем:

. (3)

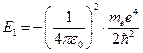=13,6 эВ,

тогда .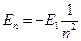

Графически схему энергетических уровней можно изобразить следующим образом:

Первый «невозбужденный» уровень соответствует энергии -13,6 эВ, второй уровень имеет энергию в четыре раза меньшую, равную – 3,4 эВ и так далее (Рис.23).

Рис.23

Теория Бора была в своё время крупным прорывом в развитии теории атома. Она с полной отчетливостью показала неприменимость классических законов к внутриатомным процессам. Однако попытки применить эту теорию к атомам, имеющим на орбите больше одного электрона, потерпели неудачу, поэтому ее называют теорией водородоподобного атома. Водородоподобным называют ион только с одним электроном на орбите и заряд ядра, которого равен Z. В этом случае выражения для радиуса орбит и энергии разрешенных орбит имеют вид:

,

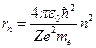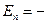
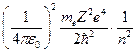
Неудачи теории Бора были обусловлены ее внутренней противоречивостью. Она не была последовательно классической, но и не была квантовой теорией. После открытия волновых свойств вещества стало совершенно ясно, что теория Бора, опирающаяся на классическую механику, могла быть только переходным этапом на пути создания последовательной теории атомных процессов.

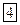Итак, простейшим атомом является атом водорода, который состоит из положительного ядра, заряд которого равене, а масса примерно на три порядка больше массы электрона, и вращающегося вокруг него электрона. Строго говоря, ядро и электрон движутся вокруг общего центра масс, но так как ядро намного тяжелее электрона, его можно считать неподвижным. Спектр излучения изолированного атома является линейчатым, т.е. состоит из целого набора разноцветных линий. Причем местоположение этих линий на шкале частот постоянно и не зависит от того, каким способом был получен атомарный газ.

Еще в 1885 году, изучая видимую часть спектра атомарного водорода, швейцарский физик Бальмер обнаружил, что длины волн и частоты этих линий могут быть рассчитаны по формулам:

,

,

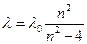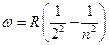где 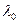- некоторая константа; n=3,4,5 …

Согласно постулату Бора, переход электрона из одного стационарного состояния с квантовым числом n и энергией 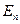в другое c квантовым числом m (n>m) и энергией 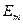сопровождается излучением кванта с энергией:

.

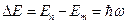Соответственно, частота этого кванта равна: .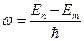

Подставив в него выражения для 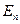и 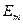, получим:

.

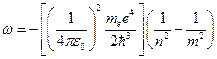Обозначим через Rмножитель, стоящий перед круглой скобкой. Так как в него входят только константы, то Rбудет тоже константой, которую называют постоянной Ридберга.

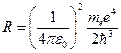=2,07 .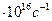

В результате получим:

.

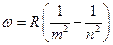Мы получили, по сути, формулу Бальмера.

Дальнейшие исследования показали, что в спектре излучения атома водорода

линии можно объединить в несколько серий.

Рис.24

Спектр атома водорода.

В ультрафиолетовой области лежит серия Лаймана, линии этой серии возникают при переходе электрона с любого уровня на первый:

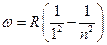, n = 2,3,4…

Видимая часть спектра – серия Бальмера, она возникает при переходе электрона с любого уровня на второй:

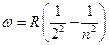, n = 3,4,5…

Все остальные серии лежат в инфракрасной области спектра:

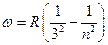, n = 4,5,6… серия Пашена,

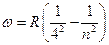, n = 5,6,7… серия Брэкета,

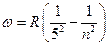, n = 6,7,8… серия Пфунда.

Итак, модель Бора дала возможность:

- объяснить линейчатость спектров испускания и поглощения отдельных атомов;

- гарантировала устойчивость атома;

- позволила рассчитать энергию ионизации для атома водорода.

Энергия ионизации - это энергия, которую необходимо затратить, чтобы оторвать электрон от ядра без создания у него начального запаса кинетической энергии.

С другой стороны:

- основные положения теории постулировались, а не доказывались;

- не позволила объяснить не только спектры других атомов, но даже спектр молекулы водорода.

ЛЕКЦИЯ 6

АТОМНАЯ ФИЗИКА (продолжение)

5. Квантовомеханическая модель атома водорода.

6. Магнитный и механический момент электрона. Гиромагнитное отношение.

7. Спин электрона.

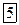Рассмотрим задачу о построении модели атома водорода с квантовомеханической точки зрения.

Электрон в атоме имеет потенциальную энергию равную:

,

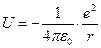где r – расстояние от электрона до ядра.

Стационарное уравнение Шрёдингера для этого случая имеет вид:

.

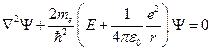Поле, в котором движется электрон, является центрально симметричным, тогда стационарное уравнение Шрёдингера в сферических координатах будет иметь вид:

,

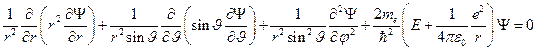где 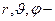сферические координаты.

Можно показать, что приведенное уравнение имеет однозначные, конечные и непрерывные решения в двух случаях:

1. при любых значениях Е>0

2. при дискретных отрицательных значениях энергии Е равных:

.

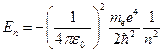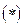
Причём первый случай соответствует электрону, пролетающему мимо ядра, второй, с 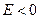, соответствует электрону, находящемуся в пределах атома.

Сравнив уравнение со звездочкой с уравнением (3) из предыдущей лекции, видим, что квантовая механика получила те же результаты, что и теория Бора. Но квантовая механика, в отличии от теории Бора, пришла к ним логическим путем из решения уравнения Шрёдингера.

Собственные функции, являющиеся решениями уравнения Шрёдингера образуют счетное множество, каждой функции из которого присваивается трехзначный номер(n,l,m).

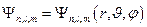
n – принимает целые значения от 1 до 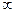и называется главным квантовым числом. Оно определяет возможные (разрешенные) значения энергии электрона в атоме.