Модуль собственного механического момента определяется спиновым квантовым числом s, которое равно .
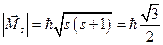 .
.
Проекция спина на заданное направление может принимать квантованные значения, отличающиеся друг от друга на .
Где .
Существование собственного механического момента у электрона (заряженной частицы) дало возможность предположить наличие у него и собственного магнитного момента. Гиромагнитное отношение для собственных механического и магнитного моментов электрона оказалось в два раза больше, чем такое же отношение для орбитальных моментов.
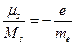 .
.
Откуда модуль собственного магнитного момента электрона равен:
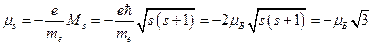 .
.
Проекция спинового магнитного момента электрона на ось Z может иметь два значения:
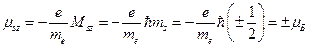 .
.
Полный механический момент электрона 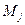 является векторной суммой орбитального и собственного механических моментов:
является векторной суммой орбитального и собственного механических моментов:
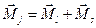 ,
,
Модуль полного момента импульса можно представить в виде:
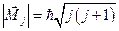 ,
,
где j – квантовое число, принимающее значения : 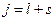 или
или 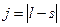 , где
, где 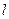 и s – орбитальное и спиновое квантовые числа.
и s – орбитальное и спиновое квантовые числа.
Полный магнитный момент электрона определяется более сложным соотношением. Это связано с тем, что коэффициент пропорциональности между собственными механическим и магнитным моментами в два раза превышает аналогичный коэффициент для орбитальных моментов.
Соответствующий расчет дает следующее соотношение: 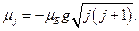 ,
,
где g – множитель Ланде, равный:
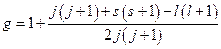 .
.
Рассмотрим, как существование спина объясняет расщепление энергетических уровней и, соответственно, расщепление спектральных линий.
Орбитальный и спиновой магнитные моменты взаимодействуют друг с другом подобно тому, как взаимодействуют две магнитные стрелки. Это взаимодействие называется спин-орбитальным. Их энергия взаимодействия зависит от взаимной ориентации орбитального магнитного момента 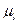 и спинового магнитного момента
и спинового магнитного момента 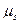 . Из этого можно сделать вывод, что состояния с разными значениями полного магнитного момента должны обладать разной энергией. Если
. Из этого можно сделать вывод, что состояния с разными значениями полного магнитного момента должны обладать разной энергией. Если 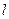 =0, то квантовое число
=0, то квантовое число 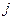 имеет только одно значение, равное
имеет только одно значение, равное 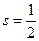 ; и эти уровни не расщепляются. При
; и эти уровни не расщепляются. При 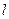 =1 ,
=1 , 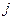 может принимать значения
может принимать значения 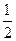 или
или 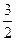 и уровень, следовательно, и спектральная линия расщепляется на две; и т.д.
и уровень, следовательно, и спектральная линия расщепляется на две; и т.д.
Вектора полного механического момента 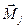 и полного магнитного момента
и полного магнитного момента  электрона не колинеарны.
электрона не колинеарны.
Выводы:
1. В квантовой механике стационарные состояния электрона в атоме водорода описываются с помощью четырех квантовых чисел: n – главное квантовое число, определяющее энергию стационарного состояния; 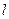 - орбитальное квантовое число, определяющее орбитальные механический и магнитный моменты электрона; m
- орбитальное квантовое число, определяющее орбитальные механический и магнитный моменты электрона; m 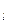 - магнитное квантовое число, которое позволяет вычислить проекции орбитальных механического и магнитного моментов на направление внешнего магнитного поля;
- магнитное квантовое число, которое позволяет вычислить проекции орбитальных механического и магнитного моментов на направление внешнего магнитного поля;
спинового квантового числа s, которое характеризует собственные механический и магнитный моменты электрона.
2. Полные механический и магнитный моменты электрона определяются квантовым числом j , величина которого зависит от значений 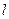 и s.
и s.
ЛЕКЦИЯ 7
МНОГОЭЛЕКТРОННЫЕ АТОМЫ И МОЛЕКУЛЫ.
1. Полный механический и магнитный моменты атома.
2. Опыт Штерна и Герлаха.
3. Принцип Паули.
4. Энергия молекул.
.
 Полная потенциальная энергия электрона в многоэлектронном атоме определяется как взаимодействием электрона с ядром, так и его взаимодействием с другими электронами.
Полная потенциальная энергия электрона в многоэлектронном атоме определяется как взаимодействием электрона с ядром, так и его взаимодействием с другими электронами.
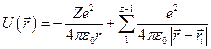 ,
, 
где Z – число электронов в атоме, которое равно порядковому номеру элемента в таблице Менделеева; 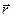 - радиус-вектор, определяющий положение данного электрона по отношению к ядру;
- радиус-вектор, определяющий положение данного электрона по отношению к ядру; 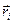 - радиус-векторы, определяющие положение других электронов.
- радиус-векторы, определяющие положение других электронов.
Первое слагаемое в выражении 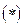 определяет энергию взаимодействия электрона с ядром, второе – энергию его взаимодействия с другими электронами.
определяет энергию взаимодействия электрона с ядром, второе – энергию его взаимодействия с другими электронами.
Линейная скорость электрона в атоме велика, поэтому можно считать, что электрон движется в усредненном силовом поле, созданном ядром и остальными электронами. Это поле будет сферически симметричным:
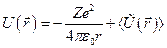 ,
,
где 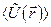 - усредненная потенциальная энергия взаимодействия одного электрона, находящегося на расстоянии
- усредненная потенциальная энергия взаимодействия одного электрона, находящегося на расстоянии 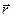 от ядра с другими электронами.
от ядра с другими электронами.
В данном случае полная энергия электрона в стационарном состоянии будет зависеть не только от главного квантового числа n,но и от орбитального 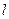 :
:
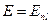
Механический и магнитный моменты атома складываются из орбитальных и спиновых механических и магнитных моментов электронов.
Атомное ядро тоже обладает магнитным моментом, но он на три порядка меньше, чем у электрона и существенного влияния на конечный результат не оказывает.
Результирующий орбитальный (механический) момент атома определяется атомным орбитальным квантовым числом L:
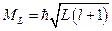 ,
,
В случае двух электронов Lможет принимать значения: 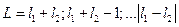 , где
, где 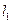 и
и 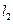 - орбитальные квантовые числа электронов.
- орбитальные квантовые числа электронов.
Проекция орбитального механического момента атома на направление OZ равна:
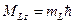
где 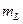 - может принимать значения
- может принимать значения 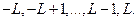
Результирующий спиновый момент и его проекция на ось Z , определяются следующими соотношениями:
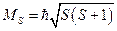 и
и 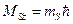
Квантовое число Sрезультирующего спинового момента атома может быть целым или полуцелым в зависимости от того, каким является число электронов в атоме - четным или нечетным. При четном числе электроновN квантовое число Sпринимает с все целые значения от 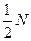 (все
(все 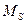 «параллельны» друг другу) до нуля (все
«параллельны» друг другу) до нуля (все 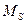 попарно компенсируют друг друга).
попарно компенсируют друг друга).
При нечетном N квантовое число Sпринимает все полуцелые значения от 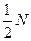 (все
(все 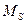 «параллельны» друг другу) до
«параллельны» друг другу) до 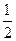 (все
(все 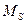 , кроме одного, попарно компенсируют друг друга).
, кроме одного, попарно компенсируют друг друга).
Результирующие орбитальный и спиновый механические моменты атома образуют в сумме полный момент импульса атома, который вычисляется по формуле:
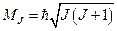 .
.
При данных 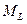 и
и 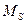 квантовое число Jможет иметь одно из следующих значений :
квантовое число Jможет иметь одно из следующих значений :
J = L+S, L+S-1,…, 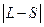 .
.
Следовательно, J будет целым, если S – целое число (при четном числе электронов в атоме) и полуцелым, если S – полуцелое (при нечетном числе электронов в атоме).
Проекция полного механического момента атома на направление Z может быть определена из:
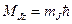 ,
,
где 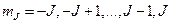 .
.
С механическими моментами связаны магнитные моменты, которые взаимодействуют между собой. Поэтому энергия атома зависит от взаимной ориентации моментов 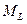 (т.е. от квантового числа L), от взаимной ориентации моментов
(т.е. от квантового числа L), от взаимной ориентации моментов 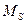 (от квантового числа S) и от взаимной ориентации
(от квантового числа S) и от взаимной ориентации 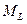 и
и 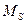 (от квантового числа J).
(от квантового числа J).
Из этого можно сделать вывод, что состояние атома и его энергия определяются квантовыми числами L, Sи J.
 В 1922 году немецкие физики Штерн и Герлах экспериментально доказали, что магнитные моменты атомов тоже являются величинами квантованными. В их опытах пучок атомов пропускался через сильно неоднородное магнитное поле (рис.27). Высокая неоднородность достигалась за счет специальной формы полюсных наконечников.
В 1922 году немецкие физики Штерн и Герлах экспериментально доказали, что магнитные моменты атомов тоже являются величинами квантованными. В их опытах пучок атомов пропускался через сильно неоднородное магнитное поле (рис.27). Высокая неоднородность достигалась за счет специальной формы полюсных наконечников.
В неоднородном магнитном поле на атомы, поскольку они состоят их заряженных частиц, должна действовать сила, проекция которой на ось ОХ определяется выражением:
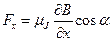 ,
,
где 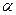 - угол между направлениями магнитного момента атома и вектором индукции магнитного поля B.
- угол между направлениями магнитного момента атома и вектором индукции магнитного поля B.
Рис. 27.
Схема опыта Штерна и Герлаха.
1,2 - наконечники полюсов электромагнита; 3 – экран.
При хаотическом распределении магнитных моментов по направлениям в пучке значения угла 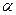 меняются в пределах от 0 до
меняются в пределах от 0 до 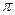 . В соответствии с этим, предполагалось, что узкий пучок атомов после прохождения между полюсами электромагнита образует на экране сплошной растянутый след, края которого соответствуют атомам, моменты которых были ориентированы под углами
. В соответствии с этим, предполагалось, что узкий пучок атомов после прохождения между полюсами электромагнита образует на экране сплошной растянутый след, края которого соответствуют атомам, моменты которых были ориентированы под углами 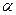 =0 и
=0 и 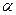 =
= 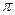 .
.
Рис. 28.
Однако, вместо сплошного растянутого следа на экране получились отдельные линии, расположенные симметрично относительно следа полученного без магнитного поля.
Опыт Штерна и Герлаха показал, что углы, под которыми ориентируются магнитные моменты атомов в магнитном поле, могут иметь только дискретные значения, т.е. проекция магнитного момента атома на направление магнитного поля квантуется.
Для магнитных моментов атомов измерения дали значения порядка нескольких магнетонов Бора. Атомные пучки некоторых элементов не дали расщепления на отдельные линии (ртуть, магний), что указывало на то, что атомы этих элементов не имеют магнитных моментов.
 В классической механике частицы одинаковой природы (например, электроны) можно различать. Пронумеровав их в некоторый момент времени можно следить за каждой из них при её движении по траектории и в любой момент времени указать, какой номер был присвоен той или иной частице.
В классической механике частицы одинаковой природы (например, электроны) можно различать. Пронумеровав их в некоторый момент времени можно следить за каждой из них при её движении по траектории и в любой момент времени указать, какой номер был присвоен той или иной частице.
В квантовой механике в силу принципа неопределенности следить за частицей невозможно, так как траектория её непредсказуема. Следовательно, квантовые частицы оказываются неразличимы. Это утверждение носит название принципа тождественности одинаковых частиц.
Существование этого принципа приводит к серьёзным физическим выводам.
Пусть система состоит из двух тождественных частиц. Совокупность параметров, определяющих одну из частиц, обозначим 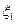 ; вторую
; вторую 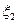 . Волновая функция, описывающая данную систему, представлена в виде
. Волновая функция, описывающая данную систему, представлена в виде 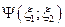 . Так как частицы неразличимы, то перестановка
. Так как частицы неразличимы, то перестановка 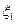 и
и 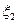 не приведет к изменению свойств системы и, следовательно,
не приведет к изменению свойств системы и, следовательно, 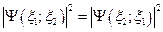 .
.
При этом возможны два случая :
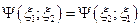 - функции являются симметричными; и они описывают частицы с нулевым или целым спином.
- функции являются симметричными; и они описывают частицы с нулевым или целым спином.
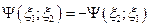 - функции антисимметричны; частицы, которыми они описываются, имеют полуцелый спин.
- функции антисимметричны; частицы, которыми они описываются, имеют полуцелый спин.
В квантовой механике доказывается, что частицы, имеющие нулевой или целый спин, подчиняются статистике Бозе-Эйнштейна и называются «бозоны». Они могут находиться в пределах системы в одинаковом состоянии в неограниченном количестве, поэтому их еще называют «коллективистами». К таким частицам относятся фотоны и 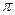 -мезоны.
-мезоны.
Частицы с полуцелым спином в одном квантовом состоянии могут находиться только по одиночке. Такие частицы (электроны, протоны, нейтроны)являются индивидуалистами, подчиняются статистике Ферми-Дирака и называются « фермионами».
Для этих частиц в 1925 году Вольфганг Паули сформулировал принцип запрета, согласно которому:
в одном и том же атоме или любой другой квантовой системе не может быть одновременно двух электронов или любых других частиц с полуцелым спином, обладающих одинаковым набором квантовых чисел.
То есть, в атоме не может одновременно быть двух электронов с одинаковыми 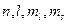 .
.
Принцип запрета Паули составляет основу понимания не только структуры сложных атомов, но и природы молекул, химической связи и ряда других явлений.
Этот принцип дает объяснение периодичности свойств атомов и объясняет последовательность элементов в таблице Менделеева.
Рассмотрим строение некоторых простых атомов в основном состоянии. Следующий за атомом водорода атом гелия He имеет два электрона. Оба электрона могут иметь главное квантовое число n = 1, 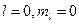 , но спиновые числа у них разные:
, но спиновые числа у них разные: 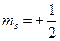 и
и 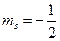 .
.
У лития Li три электрона, два из которых могут находиться в состоянии с n = 1. Но у третьего электрона главное квантовое число не может быть равным единице, так, как в этом случае нарушался бы принцип Паули, следовательно, у него n = 2 , 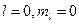 поскольку рассматриваемый атом должен находится в основном состоянии. Состояния с другими значениями
поскольку рассматриваемый атом должен находится в основном состоянии. Состояния с другими значениями 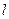 и
и 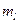 будут возбужденными.
будут возбужденными.
 Экспериментально установлено, что силы, удерживающие атомы в молекуле, вызваны взаимодействием внешних электронов. Электроны внутренних оболочек при объединении атомов в молекулу остаются в прежних состояниях.
Экспериментально установлено, что силы, удерживающие атомы в молекуле, вызваны взаимодействием внешних электронов. Электроны внутренних оболочек при объединении атомов в молекулу остаются в прежних состояниях.
Мы ограничимся рассмотрением двухатомных молекул.
Различают два вида связи между атомами в молекуле.
Ый вид – гетерополярная или ионная связь. В этом случае электроны распределяются так, что около одного из ядер образуется избыток электронов (отрицательный ион), а около другого недостаток (положительный ион).
Ой вид – гомеополярная или ковалентная связь. Она образуется парами внешних (валентных) электронов двух атомов ( по одному от каждого атома), которые вращаются одновременно около обоих ядер.
В 1927 году немецкие физики Гайтлер и Лондон впервые рассчитали основное состояние молекулы водорода 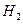 . Оказалось, что образование молекулы возможно лишь при сближении атомов с антипараллельными спинами и что собственные значения энергии молекулы зависят от расстояния между ядрами атомов.
. Оказалось, что образование молекулы возможно лишь при сближении атомов с антипараллельными спинами и что собственные значения энергии молекулы зависят от расстояния между ядрами атомов.
В основном изменение энергетического запаса молекулы происходит в результате изменения электронной конфигурации в периферической части молекулы.
При заданной электронной конфигурации молекулы ядра могут различным образом колебаться и вращаться около общего центра масс. С этими видами движения связаны запасы колебательной и вращательной энергий.
В первом приближении все виды движений в молекуле можно считать независимыми, т.е.:
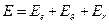 ,
,
где  электронная энергия, связанная с конфигурацией электронных оболочек,
электронная энергия, связанная с конфигурацией электронных оболочек,
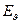 - колебательная (вибрационная) энергия,
- колебательная (вибрационная) энергия,
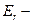 вращательная или ротационная энергия.
вращательная или ротационная энергия.
Поскольку атомы в молекуле в первом приближении можно рассматривать как гармонические осцилляторы, колебательную энергию можно определить следующим соотношением:
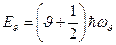 ,
,
где 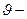 колебательное квантовое число; (при рассмотрении квантового осциллятора соответствующее квантовое число мы обозначали n), принимающее значения
колебательное квантовое число; (при рассмотрении квантового осциллятора соответствующее квантовое число мы обозначали n), принимающее значения 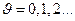 ;
;
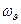 - частота колебаний.
- частота колебаний.
В данном случае остается справедливым правило отбора для квантового осциллятора
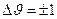 .
.
То есть, для молекулы возможен переход только между соседними колебательными энергетическими уровнями.
Запас вращательной энергии можно определить:
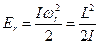 ,
, 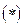
где I – момент инерции молекулы, 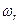 - частота вращения молекулы.
- частота вращения молекулы.
В 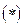
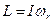 - момент импульса молекулы, который может принимать только дискретные значения, определяемые квантовым числом J = 0,1,2,…, которое подчиняется следующему правилу отбора
- момент импульса молекулы, который может принимать только дискретные значения, определяемые квантовым числом J = 0,1,2,…, которое подчиняется следующему правилу отбора 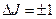 .
.
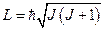 .
.
Вращательная энергия связана с квантовым вращательным числом J соотношением:
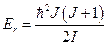 .
.
На основании выше изложенного, полную энергию молекулы можно записать:
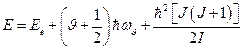 .
.
Эксперименты и расчеты показывают, что расстояние между вращательными уровнями 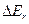 значительно меньше, чем расстояния между колебательными уровнями
значительно меньше, чем расстояния между колебательными уровнями 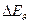 , которое в свою очередь значительно меньше расстояния между электронными уровнями
, которое в свою очередь значительно меньше расстояния между электронными уровнями 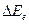 . Следовательно, в первую очередь при внешнем воздействии меняется энергия вращательного движения, затем колебательного. Для того чтобы изменить электронную конфигурацию молекулы воздействие должно быть очень сильным.
. Следовательно, в первую очередь при внешнем воздействии меняется энергия вращательного движения, затем колебательного. Для того чтобы изменить электронную конфигурацию молекулы воздействие должно быть очень сильным.
ЛЕКЦИЯ 8
МНОГОЭЛЕКТРОННЫЕ АТОМЫ И МОЛЕКУЛЫ
(продолжение)
5. Спектры атомов и молекул.
6. Рентгеновские спектры.
7. Вынужденное излучение. Лазеры.
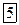 Спектры излучения и поглощения изолированных атомов представляет собой набор из отдельных спектральных линий, поэтому они называется линейчатым.
Спектры излучения и поглощения изолированных атомов представляет собой набор из отдельных спектральных линий, поэтому они называется линейчатым.
Спектральные линии возникают при переходе атома с одного разрешенного энергетического состояния в другое. Спектры поглощения возникают при переходе электронов с энергетического состояния меньшим номером (n) в состояние с большим номером (m), при этом электрон поглощает квант, энергия которого равна разности энергий состояний между которыми происходит переход.
. 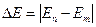 .
.
Они представляют собой набор темных линий на цветном фоне.
Спектры испускания возникают при переходе электронов с уровня, у которого большая энергия в состояние с меньшей энергией. При этом электрон испускает квант света, энергия которого соответствует разности энергий разрешенных уровней, между которыми происходит переход.
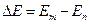 .
.
Поскольку для каждого химического элемента набор разрешенных переходов строго индивидуален, то по положению спектральных линий можно судить о том, какой элемент дал тот или иной спектр.
Молекулярные спектры при наблюдении в прибор средней разрешенной способности представляются в виде полос. При применении приборов с высокой разрешающей способностью видно, что полосы состоят из большого числа близко расположенных друг к другу линий.
В зависимости от того, изменение каких видов энергии обуславливает испускание молекулой фотона, различают три вида полос:
- вращательные;
- колебательно-вращательные;
- электронно-колебательные.
Поскольку 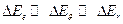 , то при слабых возмущениях меняется только
, то при слабых возмущениях меняется только 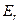 ; при сильных
; при сильных 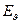 . При очень сильных может меняться электронная конфигурация, а, следовательно, и
. При очень сильных может меняться электронная конфигурация, а, следовательно, и 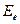 .
.
Ограничимся рассмотрением первых двух типов спектральных полос для двух атомной молекулы.
Как мы уже знаем, полная энергия молекулы состоит из электронной, колебательной и вращательной энергий:
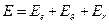
В основном состоянии молекулы все виды энергий имеют минимальные значения. При сообщении молекуле достаточного количества энергии она переходит в возбужденное состояние и затем, совершая разрешенный правилами отбора переход в одно из низших энергетических состояний, излучает фотон с энергией 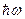 .
.
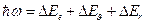 ,
,
где 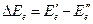 ;
;
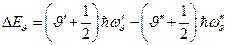 ;
;
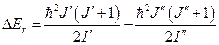 .
.
Дата добавления: 2015-08-08; просмотров: 1998;
