Число называется орбитальным квантовым числом и, при заданном n, оно принимает целые значения от 0 до n-1.

Орбитальное квантовое число позволяет вычислить модуль вектора орбитального момента импульса L(механический момент) электрона в атоме.

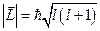
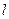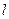Число m называют магнитным квантовым числом; оно принимает целые значения от - до + и характеризует проекцию орбитального момента импульса на направление внешнего магнитного поля, которое принимается за ось Z.

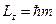
Поэтому постоянную Планка можно считать естественной единицей момента импульса.

Каждому значению главного квантового числа (кроме 1) соответствует несколько собственных значений волновой функции 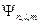, отличающихся значениями 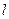и m.

Состояния, имеющие одинаковое главное квантовое число, но разные орбитальное и магнитное квантовые числа, называются вырожденными, а число этих состояний – кратностью вырождения N.

.

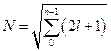Итак, мы получили, что момент импульса электрона и его проекция на ось Z, так же как энергия являются величинами квантованными.

Испускание и поглощение кванта происходит при переходе электрона с одного уровня на другой. В квантовой механике доказывается, что возможны только такие переходы, при которых орбитальное квантовое число 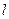изменяется на единицу.

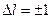
Это условие называется правилом отбора. Существование правила отбора обусловлено наличием у излученного или поглощенного фотона собственного момента импульса, равного примерно . Так что, правило отбора есть следствие закона сохранения момента импульса.

Мы получили, что квантовая теория строения атома сохраняет некоторые аспекты теории

Бора. Например, электроны могут находиться в атоме только в дискретных состояниях с определенной энергией; при переходе электрона из одного состояния в другое испускается ( или поглощается) фотон. Но использование вероятностного подхода позволило квантовой механике представить совсем иную картину строения атома.

В квантовой теории не существует вполне определенных круговых орбит электронов. В силу волновой природы, электрон «размазан» в пространстве, подобно облаку отрицательного заряда. Размеры и форму электронного облака определяют квантовые числа. Для основного состояния атома водорода решение уравнения Шрёдингера дает волновую функцию вида:

,

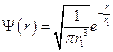где 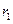- постоянная, численно равная радиусу первой боровской орбиты, 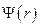- волновая

функция, зависящая только от расстояния от электрона до ядра r и не зависящая от углов .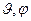

Это показывает, что электронное облако атома водорода в основном состоянии сферически-симметрично.

а) n =1; 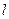=0; m = 0. б) n =2; 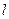=0; m = 0. в) n = 2; 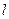=1; m = 1

Рис.25

Электронное облако, или распределение плотности вероятности для электрона в атоме водорода.

Однако не всегда электронные облака имеют сферически-симметричную форму. Хотя энергетические уровни слабо зависят от орбитального и магнитного квантовых чисел, они влияют на функцию распределения плотности вероятности. При n = 1 квантовые числа 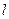и

m могут принимать только нулевые значения и электронное облако имеет сферическую форму, Рис.25а. При n =2; 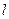=0; m = 0 появляются два сферических облака распределения вероятности, рис.25б; при n = 2; 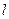=1; m = 1 функция распределения вероятности перестает иметь сферическую форму и по форме напоминает гантель, рис 25в.

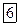Классическая заряженная частица, движущаяся по круговой орбите, обладает механическим моментом (момент импульса) L и магнитным моментом 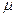. В прошлом семестре мы получили, что отношение этих моментов для электрона равно:

.

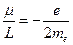Это выражение называется гиромагнитным отношением. Оно было получено в предположении, что электрон движется по классическим законам.

В квантовой механике понятие траектории (как орбиты электрона) утрачивает смысл.

Однако магнитный и механический моменты, обусловленные движением электрона вокруг ядра, по-прежнему называют орбитальными. Экспериментально установлено, что гиромагнитное соотношение, полученное в классической механике, справедливо и в квантовой теории.

В дальнейшем для удобства будем обозначать механический момент электрона буквой М.

,

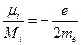где 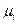и 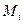- орбитальные магнитный и механический моменты электрона, соответственно. Знак минус указывает на то, что направление магнитного и механического моментов противоположны.

Модуль орбитального механического момента равен:

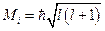, где 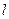-орбитальное квантовое число электрона. Проекция орбитального механического момента на направление Z определяется выражением:

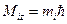, где m 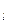- магнитное квантовое число.

Постоянную Планка можно считать естественной единицей механического момента.

Рис 26

Из гиромагнитного соотношения следует, что орбитальный магнитный момент электрона равен:

.

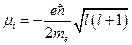Множитель 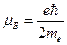=0,927 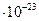Дж/Тл называется магнетоном Бора и представляет собой естественную единицу магнитного момента.

Проекция орбитального магнитного момента электрона на направление ОZ равна:

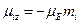
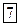Исследование спектров водорода с помощью приборов с большой разрешающей способностью показало, что каждая линия его спектра является двойной, их называют дуплетами. Расщепление спектральных линий, очевидно, обусловлено расщеплением энергетических уровней.

Для объяснения этого эффекта Гаудсмит и Уленбек в 1925 году выдвинули гипотезу о том, что электрон обладает и собственным механическим моментом, не связанным с его вращением вокруг ядра. Этот собственный механический момент был назван спином .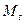

Существование спина вытекает также из уравнения релятивистской квантовой механики, полученного Дираком, и удовлетворяющем всем требованиям теории относительности.

Со временем гипотеза о наличие у электрона спина была неоднократно подтверждена экспериментально.