Сложение колебаний

Колебания могут складываться и при этом усиливать или гасить друг друга, или изменять траекторию движения тела. Рассмотрим сложение колебаний, совершаемых в одном направлении. Пусть осциллятор совершает два одновременных колебания в одном направлении и одинаковой частоты ω₀:

x₁=A₁cos(ω₀t+a₁) и x₂=A₂cos(ω₀t+a₂).

При этом суммарное колебание координаты x(t) равно x = x₁ + x₂. 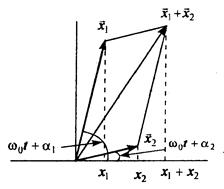Представим колебания x₁ и x₂ в виде векторов на плоскости (рис.), модулями которых являются амплитуды колебаний, а фазы колебаний будут служить углами наклона векторов к оси x. При изменении времени векторы x₁ и x₂, будут равномерно вращаться в плоскости рисунка, однако разность фаз между колебаниями остается неизменной. Из рисунка видно, что вектор x = x₁ + x₂, представляет собой сумму колебаний x₁ и x₂. В самом деле, проекции векторов x₁, и x₂, на ось x соответственно равны A₁cos(ω₀t+a₁) и А₂cos(ω₀t+a₂), а проекция вектора x равна сумме этих проекций. Результирующее колебание также можно записать в виде: x(t)=x₁+x₂= = Acos(ω₀t+a). Частота результирующего колебания равна частоте складываемых колебаний, т. е. результирующее колебание также гармоническое. Амплитуду результирующего колебания нетрудно найти из рис.

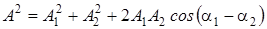, (3.15)

а новую начальную фазу определить так:

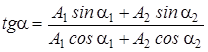. (3.16)

Из формулы (3.15) следует, что амплитуда результирующего колебания существенно зависит от значения разности фаз начальных колебаний. Если разность фаз a₁–a₂=0, колебания находятся в фазе, и амплитуды A₁ и A₂ складываются A = A₁ + A₂. Если же разность фаз равна ±p, колебания находятся в противофазе, т.е. амплитуда результирующего колебания A = |A₁ – A₂|.

Выше было рассмотрено сложение двух колебаний с одинаковой частотой, при этом результирующее колебание осталось гармоническим с той же частотой. Если складываются колебания разной частоты, то векторы x₁ и x₂ в плоскости будут вращаться с разной скоростью (рис.). Тогда результирующий вектор в процессе вращения будет изменяться по величине и описывать сложное негармоническое колебание.

Рассмотрим сложение колебаний во взаимно перпендикулярных направлениях. Наиболее простым примером такого колебания являются одновременные колебания частицы в направлениях x и y, происходящие с одинаковыми частотами и амплитудами (см. формулы (3.11)). Как было установлено, результирующее движение представляет собой равномерное вращение в плоскости по окружности с радиусом, равным амплитудам колебаний величин x и y. В случае неравных амплитуд и частот элементарных колебаний результирующее движение может происходить по весьма сложным траекториям и не будет гармоническим.

Таким образом, сложение гармонических колебаний с различными частотами и амплитудами позволяет осуществить колебание произвольной формы. Это обстоятельство используется для создания негармонических колебаний необходимой формы. Отсюда следует и обратное утверждение: всякое сложное негармоническое колебание может быть представлено в виде суммы простых гармонических колебаний. Другими словами, движение сложной колебательной системы со многими степенями свободы можно описать, рассматривая соответствующий набор гармонических осцилляторов.

Свободные механические колебания могут существовать в системах, где сохраняется полная механическая энергия. В реальных системах всегда присутствует трение, благодаря которому свободные колебания, возбужденные первоначально в системе, со временем будут затухать. Кроме того, колебания в различных системах часто происходят под действием внешней силы — так называемой вынуждающей силы. Колебания при наличии сил трения являются затухающими, а под действием внешней силы — вынужденными.