Комплексные числа. Комплексным числом z называется число вида

Комплексным числом z называется число вида

z=x+iy, (1)

где x и y — вещественные числа, i — мнимая единица (i²=—1). Число x называется вещественной частью комплексного числа z. Символически это записывается в виде x=Rez. Число у называется мнимой частью z (записывается: y=lmz). Число

z*=x—iy.(2)

называется комплексно сопряженным числу x+iy. Вещественному числу x можно сопоставить точку на оси x.

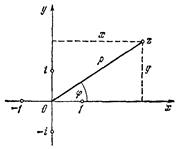Комплексному числу z можно сопоставить точку на плоскости, имеющую координаты x, y (рис.). Каждая точка плоскости определяет некоторое комплексное число z. Следовательно, комплексное число можно задать с помощью декартовых координат x и y соответствующей точки. Однако то же самое число можно задать с помощью полярных координат ρ и φ. Между обеими парами координат имеются соотношения

x = ρ∙cosφ, y = ρ∙sinφ, 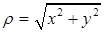, φ=arctg(y/x). (3)

Расстояние от начала координат до точки, изображающей число z, называется модулем комплексного числа (обозначается |z|). Очевидно, что

z= .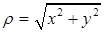

Число φ называют аргументом комплексного числа z.

Приняв во внимание соотношения (3), можно представить комплексное число в тригонометрической форме:

z=ρ(cosφ+i sinφ).

Два комплексных числа z₁=x₁+iy₁ и z₂=x₂+iy₂ считаются равными друг другу, если в отдельности равны их вещественные и мнимые части:

z₁=z₂, если x₁=x₂ и y₁=y₂.

Модули двух равных между собой комплексных чисел одинаковы, а аргументы могут отличаться лишь слагаемым, кратным 2π:

ρ₁ = ρ₂, φ₁=φ₂±2kπ.

Из выражений (1) и (2) видно, что в случае, когда z*=z, мнимая часть z есть нуль, т. е. число z оказывается чисто вещественным. Таким образом, условие вещественности числа z можно записать в виде

z* =z.

В математике доказывается соотношение

e^iφ = соsφ +isinφ, (4)

которое называется формулой Эйлера. Заменив в этой формуле φ на —φ и учтя, что cos (—φ)=cosφ, a sin(‑φ) = — sinφ, получим соотношение

e^‑iφ = соsφ ‑ i∙sinφ. (5)

Сложим выражения (4) и (5) и решим получившееся соотношение относительно cosφ. В результате имеем

соsφ = 1/2∙(e^iφ +е^‑iφ).

Вычтя (5) из (4), получим, что sinφ = (1/2i) (e^iφ ‑ e^‑iφ).

С помощью формулы (4) комплексное число можно записать в показательной форме:

z = ρe^‑iφ.

Комплексно сопряженное число в показательной форме имеет вид

z* = ρe^‑iφ.

При сложении комплексных чисел складываются отдельно их вещественные и мнимые части:

z₁+z₂=(x₁+x₂)+i(y₁+y₂).

Перемножение комплексных чисел удобно осуществлять, беря эти числа в показательной форме:

z = z₁∙z₂ = ρ₁e^iφ₁∙ρ₂e^iφ₂ = ρ₁ρ₂e^i(φ₁ ^{+ φ}₂⁾

Модули комплексных чисел перемножаются, а аргументы складываются:

ρ=ρ₁∙ρ₂, φ=φ₁+φ₂.

Аналогично осуществляется деление комплексных чисел:

легко получить, что

z∙z* = ρ².

(квадрат модуля комплексного числа равен произведению этого числа на его комплексно сопряженное).