Индуктивность в цепи переменного тока.
Рассмотрим индуктивность в цепи переменного тока. Исследуем, что произойдёт с током в цепи, если напряжение на входе изменяется по закону косинуса:
U =U0 cos wt; (12).
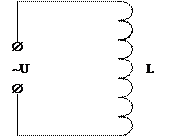 |
Рис6. Индуктивность включена в цепь переменного тока.
Известно, что ЭДС самоиндукции зависит от индуктивности L и скорости изменения тока, и определяется известной вам формулой 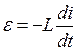 .
.
Теперь обратим внимание на то, что внешний источник напряжения и ЭДС самоиндукции включены параллельно. Следовательно, в соответствии со вторым законом Кирхгофа «Сумма падений напряжений в последовательной замкнутой цепи равна нулю.» можно составить уравнение.
Имеем уравнение: 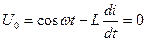 ; (13).
; (13).
Это дифференциальное уравнение 1 порядка. Переменные параметры: ток I и время t.
Для решения уравнения (13) необходимо разделить переменные и проинтегрировать.
Проведём разделение переменных: 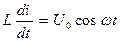 ;
; 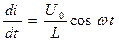
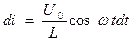 ;
;  ;
;
Проинтегрируем и имеем: 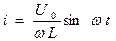 ; (14).
; (14).
Заданное напряжение на входе (12) изменяется по закону косинуса, а ток в формуле (14) изменяется по закону синуса.
Для анализа формул (12) и (14) выразим, воспользуясь тригонометрическими преобразованиями, изменения тока так же через косинус.
Тогда окончательно имеем: 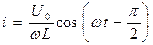 ; (15).
; (15).
Сравнение формул (12) и (15) показывает, что напряжение и ток в цепи с индуктивностью изменяются по закону косинуса.
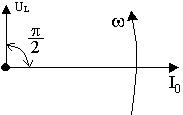 |
При этом видно, что в цепи с индуктивностью отстаёт от напряжения по фазе на угол p/2. Изобразим это на векторной диаграмме.
Рис.6. Векторная диаграмма для изменений напряжения и тока в цепи с индуктивностью.
Задерживание фазы тока на индуктивности обусловлено воздействием ЭДС самоиндукции. В формуле (15) коэффициенты, стоящие перед cos играют роль амплитудного значения тока.
То есть 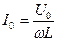 ; (16)
; (16)
Формула (16) представляет собой запись закона Ома. В этой формуле роль сопротивления играют члены, стоящие в знаменателе. Следовательно, можно записать, что XL=wL; (17).
XL – это реактивное индуктивное сопротивление. Оно не связано
с тепловыми потерями энергии. И его величина зависит от частоты и индуктивности.
Определим размерность индуктивного сопротивления XL по формуле (17).
Для определения размерности индуктивности и воспользуемся известной формулой для определения ЭДС самоиндукции 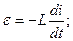 Откуда
Откуда 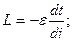 или
или 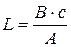 ;
;
Тогда: 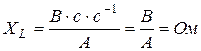 ;
;
Таким образом индуктивное сопротивление XL также как и активное R и емкостное XC измеряются в Омах.
Дата добавления: 2015-08-08; просмотров: 1317;
