Резонанс в цепи переменного тока.

Рассмотрим полную цепь переменного тока, содержащую последовательно включённые активное сопротивление R, индуктивность L, конденсатор C. Найдём выражение для полного сопротивления цепи.

Рис7. Схема последовательного соединения резистора R, конденсатора С и индуктивности L в цепи переменного тока.

Так как цепь последовательная, то в цепи образуется общий ток

i = I₀cos (wt ± j).

Приложенное напряжение U=U₀coswt распределяется между участками цепи пропорционально сопротивлению отдельных элементов.

Тогда в соответствии с законом Ома падение напряжения на отдельных элементах будет определяться формулами:

U_R=IR;

U_C=IX_C;

U_L=IX_L.

Но так как между напряжениями U_C и U_L и током I существует разность фаз, то эти напряжения должны складываться как вектора.

Строим векторную диаграмму.

U_{результ}=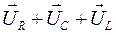

Пользуясь правилом сложения векторов найдём результирующий вектор U_{результ.}

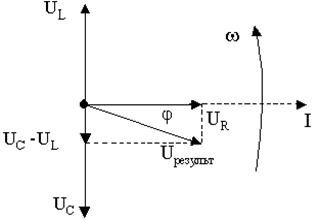Рис.8. Векторная диаграмма для последовательно соединения

R, C, L.

В результате сложения мы получили характерный треугольник напряжений. Так как в последовательной цепи ток одинаков, то можно от треугольника напряжений перейти к треугольнику сопротивлений. По теореме Пифагора результирующее падение напряжения в цепи будет определяться:

;

;

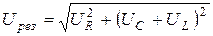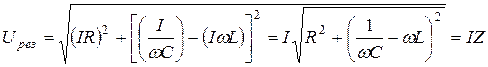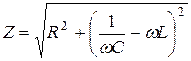; (18).

Где: Z - полное сопротивление цепи переменного тока или импеданс.

Рассмотрим резонанс напряжений в цепи переменного тока. Анализ формулы (18) показывает, что в последовательной цепи ток будет наибольшим, а сопротивление наименьшим в случае,

если X_С = X_L; то есть 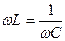; (19).

Это условие резонанса напряжений. Из формулы (19) можно получить: w ²L C =1; (20).

Решая уравнение (20) относительно w получим известную формулу Томпсона для определения резонансной частоты колебательного контура ;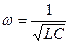

При резонансе в последовательной цепи происходит взаимная компенсация напряжений U_L и U_C каждое из которых может значительно превышать приложенное к цепи напряжение U. При этом апряжения U_L и U_C равны по величине, а их векторы направлены по одной прямой в противоположные стороны.