Конденсор в цепи переменного тока.
Рассмотрим цепь переменного тока с ёмкостью. Считаем, что других сопротивлений в цепи нет. Пусть на входе цепи действует переменное напряжение, которое изменяется по закону косинуса
U= U0coswt; (4)
Необходимо установить закон изменения тока в цепи с конденсатором. i = ?
Согласно определения емкость это есть отношение заряда к напряжению на ёмкости.
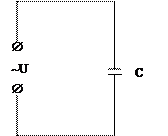 |
То есть:
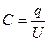 ; откуда заряд на ёмкости q=CU; (5).
; откуда заряд на ёмкости q=CU; (5).
Рис. 4: Конденсатор в цепи переменного тока.
По определению ток – это есть изменение заряда во времени.
То есть: 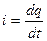 (6).
(6).
Подставим в формулу (6) вместо заряда q его величину из формулы (5) и так как на конденсаторе действует переменное напряжение, то вместо U в формуле (5) подставим переменное напряжение с заданным законом изменения U=U0 cos wt.
В результате имеем: 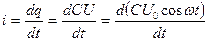 ; (7)
; (7)
Таким образом для нахождения тока в цепи с конденсатором необходимо найти первую производную от выражения (7).
Постоянные коэффициенты выносим за знак дифференцирования 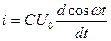 ;
;
В результате дифференцирования получаем:
i=-U0Cwsinwt; (8)
Так как заданное напряжение изменяется по закону косинуса (см. формулу 4), а ток изменяется по закону синуса (см. формулу 8), то для сравнения этих формул желательно так же выразить изменения тока через косинус.
Тогда имеем: 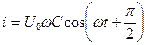 ; (9)
; (9)
Таким образом сравнение формул (4) и (9) показывает, что ток в цепи с ёмкостью опережает напряжение по фазе на угол p/2.
В полученной формуле (9) коэффициенты стоящие перед косинусом представляют собой амплитуду тока, то есть I0;
Тогда I0 = U0wС; (10)
Формула (10) по существу представляет собой запись закона Ома, так как связь между током и напряжением такова, что величина
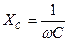 ; (11), имеет смысл сопротивления.
; (11), имеет смысл сопротивления.
XС – называется реактивным ёмкостным сопротивлением. Оно не ведёт к тепловым потерям.
Определим размерность ёмкостного сопротивления:
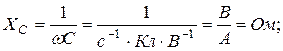 (11).
(11).
Таким образом ёмкостное сопротивление так же как обычное измеряется в Омах.
В цепях постоянного тока X ® ¥, то есть конденсатор является разрывом в цепи. В цепи переменного тока токи проводимости продолжают токи смещения диэлектрика конденсатора. Токи смещения в конденсаторе обусловлены колебательными движениями связанных зарядов в диэлектрике.
Отставание фазы напряжения от фазы тока в электротехнике принято отображать векторными диаграммами.
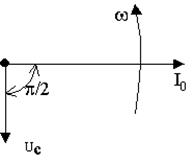 |
Рис5. Векторная диаграмма для цепи с конденсатором.
Построение векторной диаграммы начинают с изображения вектора тока I0. Затем указывают направление вращения вектора тока I0. Вектор тока I0 вращается со скоростью w против часовой стрелки. При построении вектора напряжения необходимо учитывать его отставание от вектора тока на угол 900.
Построим векторную диаграмму для цепи с конденсатором.
Напряжение на ёмкости, при отсутствии активных потерь, отстаёт от тока на угол 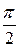 .
.
Дата добавления: 2015-08-08; просмотров: 819;
