Решение. Условие равной прочности имеет следующий вид:

Условие равной прочности имеет следующий вид:

,

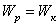где 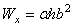; значение коэффициента определяется по таблице 4.1 и составляет для квадратного сечения ( ) .

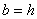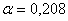Из условия равной прочности получаем:

.

Отношение весов двух валов равно отношению площадей их поперечных сечений:

.

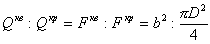Подставляя в это уравнение отношение 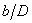из условия равной прочности, получим

.

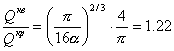Сдвиг

Сдвигомназывают деформацию, представляющую собой искажение первоначально прямого угла малого элемента бруса (рис.5.14) под действием касательных напряжений . Развитие этой деформации приводит к разрушению, называемому срезом или, применительно к древесине, скалыванием. Примером сдвига является резка полосы ножницами. На сдвиг работают жесткие соединения конструкций – сварные, заклепочные и так далее.

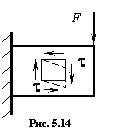
Деформация сдвига оценивается взаимным смещением граней 1 – 1 и 2 – 2 малого элемента (рис. 5.15), называемым абсолютным сдвигом и более полно –относительным сдвигом (углом сдвига)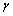

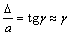, (5.19)

являющимся безразмерной величиной.

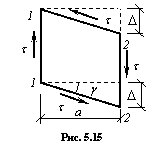
В предположении равномерного распределения касательных напряжений по сечению площадью А, они определяются по формуле

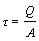, (5.20)

где Q – поперечная сила в данном сечении.

Условие прочности записывается по минимальной площади среза S_min, отражающей минимальное число соединяющих элементов (заклепок, болтов, штифтов и т.д.) или минимальную длину сварного шва.

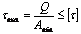
Величина допускаемых напряжений 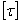зависит от свойств материала, характера нагрузки и может быть определена по 3-ей теории прочности: 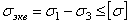, а так как при чистом сдвиге 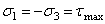, то

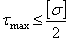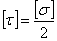, (5.21)

При расчете болтовых или заклепочных соединений учитывается смятие контактирующих поверхностей, то есть пластическую деформацию, возникающую на поверхности контакта.

,

где A_см – площадь проекции поверхности контакта на диаметральную плоскость.

При выполнении проектного расчета, то есть при определении необходимого диаметра заклепки, болта или при определении их количества необходимо учитывать условие прочности на срез и на смятие, из двух значений следует взять большее число, округлив его до ближайшего целого в меньшую сторону.

Примечания: 1. Так как болты и заклепки ослабляют соединяемые листы, последние проверяют на разрыв в ослабленных сечениях

.

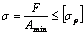При расчетах сварных швов наплывы не учитывают, а считают, что в разрезе угловой шов имеет форму прямоугольного равнобедренного треугольника и разрушение шва происходит по его минимальному сечению, высота которого

,

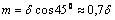где – минимальная толщина соединяемых листов.

В пределах упругости касательное напряжение прямо пропорционально относительному сдвигу

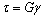(5.22)

– это закон Гука при сдвиге; G – модуль сдвига, Н/м², характеризующий жесткость материала при сдвиге.

Закон Гука при сдвиге через абсолютные деформации:

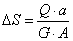, (5.23)

где а – расстояние между сдвигаемыми гранями; А – площадь грани.

Модуль сдвига G, модуль продольной упругости Е и коэффициент Пуассона 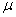материала связаны зависимостью

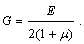
Удельная потенциальная энергия деформации сдвига равна

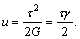
На практике чаще всего теория сдвига применяется к расчету болтов, заклепок, шпонок, сварных швов и других элементов соединений.

Расчет заклепок на срез

Мы изучали, что при простом растяжении или простом сжатии две части стержня, разделенные наклонным сечением, стремятся не только оторваться друг от друга, но и сдвинуться одна относительно другой. Растяжению сопротивляются нормальные, а сдвигу — касательные напряжения.

На практике целый ряд деталей и элементов конструкций работает в таких условиях, что внешние силы стремятся их разрушить именно путем сдвига.

В соответствии с этим при проверке прочности таких элементов на первый план выступают касательные напряжения. Простейшими примерами подобных деталей являются болтовые и заклепочные соединения. Заклепки во многих случаях уже вытеснены сваркой; однако они имеют еще очень большое применение для соединения частей всякого рода металлических конструкций: стропил, ферм мостов, кранов, для соединения листов в котлах, судах, резервуарах и т. п. Для образования заклепочного соединения в обоих листах просверливают или продавливают отверстия. В них закладывается нагретый до красного каления стержень заклепки с одной головкой; другой конец заклепки расклепывается ударами специального молотка или давлением гидравлического пресса (клепальной машины) для образования второй головки. Мелкие заклепки (малого диаметра — меньше 8 мм) ставятся в холодном состоянии (авиационные конструкции).

Для изучения работы заклепок рассмотрим простейший пример заклепочного соединения (рис.5.16). Шесть заклепок, расположенных в два ряда, соединяют два листавнахлестку. Под действием сил Р эти листы стремятся сдвинуться один по другому, чему препятствуют заклепки, на которые и будет передаваться действие сил P).

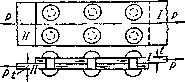
Рис.5.16.

Для проверки прочности заклепок применим общий порядок решения задач сопротивления материалов.

На каждую заклепку передаются по две равные и прямо противоположные силы: одна—от первого листа, другая — от второго. Опытные исследования показывают, что одни из заклепок ряда нагружаются больше, другие — меньше. Однако к моменту разрушения усилия, передающиеся на различные заклепки, более или менее выравниваются за счет пластических деформаций. Поэтому принято считать, что все заклепки работают одинаково. Таким образом, при 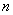заклепках в соединении, изображенном на рис.5.16, на каждую из них действуют по две равные и противоположные силы 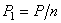(рис.5.17); эти силы передаются на заклепку путем нажима соответствующего листа на боковую полуцилиндрическую поверхность стержня. Силы 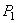стремятся перерезать заклепку по плоскости mk раздела обоих листов.

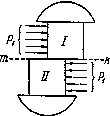
Рис.5.17.

Для вычисления напряжений, действующих по этой плоскости, разделим мысленно заклепочный стержень сечением mk и отбросим нижнюю часть (рис.5.17). Внутренние усилия, передающиеся по этому сечению от нижней части на верхнюю, будут уравновешивать силу 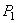т. е. будут действовать параллельно ей в плоскости сечения, и в сумме дадут равнодействующую, равную 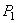. Следовательно, напряжения, возникающие в этом сечении и действующие касательно к плоскости сечения, это — касательныенапряжения . Обычно принимают равномерное распределение этих напряжений по сечению. Тогда при диаметре заклепки d на единицу площади сечения будет приходиться напряжение:

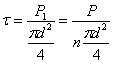
Величина допускаемого касательного напряжения 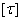, или, как говорят, допускаемого напряжения на срез, принято определять в виде: 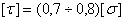. Зная 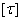, мы напишем условие прочности заклепки на перерезывание в таком виде:

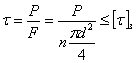
т. е. действительное касательное напряжение в материале заклепки должно быть равно допускаемому 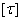, или меньше его.

Из этого условия можно определить необходимый диаметр заклепок, если задаться их числом, и наоборот. Обычно задаются диаметром заклепочных стержней d в соответствии с толщиной t склепываемых частей (обычно 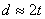) и определяют необходимое число заклепок :

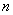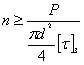
Знаменатель этой формулы представляет собой ту силу, которую безопасно может взять на себя каждая заклепка.

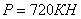
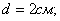
Пусть 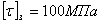; тогда

Рис.5.18

При выводе формулы расчета заклепки на перерезывание, помимо оговоренных, допущена еще одна неточность. Дело в том, что силы 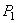действующие на заклепку, не направлены по одной прямой, а образуют пару. Эта пара уравновешивается другой парой, образующейся из реакций соединенных листов на головку заклепки (рис.5.18) и ведет к появлению нормальных напряжений, действующих по сечению mk.

Кроме этих нормальных напряжений, по сечению mk действуют еще нормальные напряжения, вызванные тем, что при охлаждении заклепочный стержень стремится сократить свою длину, чему мешает упор головок заклепки в листы. Это обстоятельство, с одной стороны, обеспечивает стягивание заклепками листов и возникновение между ними сил трения, с другой — вызывает значительные нормальные напряжения по сечениям стержня заклепки. Особых неприятностей эти напряжения принести не могут. На заклепки идет сталь, обладающая значительной пластичностью; поэтому даже если бы нормальные напряжения достигли предела текучести, можно ожидать некоторого пластического удлинения стержня заклепки, что вызовет лишь уменьшение сил трения между листами и осуществление в действительности той схемы работы заклепки на перерезывание, на которую она и рассчитывается. Поэтому эти нормальные напряжения расчетом не учитываются.

При проектировании строительных конструкций применяется следующее условие прочности на срез для заклепок и болтовых соединений

(5.24)

где Q – поперечная сила, равная внешней силе F, действующей на соединение; R_bs – расчетное сопротивление на срез; – расчетная площадь сечения болта или заклепки; d – диаметр заклепки или наружный диаметр болта; n_s – число срезов одного болта или заклепки; 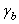– коэффициент условий работы соединения, имеющий значения в интервале ; n – число болтов или заклепок.

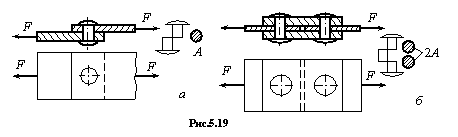
Если величины F, R_bs, 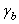, n_s известны, то задаваясь числом заклепок или болтов n, можно найти необходимый для обеспечения прочности на срез диаметр

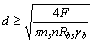. (5.25)

А зная d, F, R_bs, 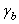, n_s, можно определить потребное число заклепок или болтов

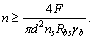(5.26)