Кручение бруса с некруглым поперечным сечением
Определение напряжений в брусе с некруглым поперечным сечением представляет собой сложную задачу, которая не может быть решена методами сопротивления материалов. Причина заключается в том, что для некруглого поперечного сечения упрощающая гипотеза плоских сечений, оказывается неприемлемой. В данном случае поперечные сечения существенно искривляются, в результате чего заметно меняется картина распределения напряжений.
Таким образом, при определении углов сдвига, в данном случае, необходимо учитывать не только взаимный поворот сечений, но и деформации сечений в своей плоскости, связанная с искривлением сечений.
Задача резко усложняется тем, что для некруглого сечения, напряжения должны определяться как функции уже не одного независимого переменного 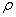 , а двух - x и y.
, а двух - x и y.
Отметим некоторые особенности законов распределения напряжений в поперечных сечениях некруглой формы. Если поперечное сечение имеет внешние углы, то в них касательные напряжения должны обращаться в нуль. Если наружная поверхность бруса при кручении свободна, то касательные напряжения в поперечном сечении, направленные по нормали к контуру также будут равны нулю.
На рис. 4.3 показана, полученная методом теории упругости, эпюра касательных напряжений для бруса прямоугольного сечения. В углах, как видно, напряжения равны нулю, а наибольшие их значения возникают по серединам больших сторон:
в точке А
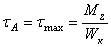 , (5.16)
, (5.16)
где  - момент сопротивления при кручении, аналог полярного момента сопротивления поперечного сечения прямоугольного бруса;
- момент сопротивления при кручении, аналог полярного момента сопротивления поперечного сечения прямоугольного бруса;

Рис. 5.13
в точке В
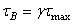 , (5.17)
, (5.17)
здесь необходимо учесть, что b - малая сторона прямоугольника.
Значения угла закручивания определяется по формуле:
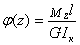 , (5.18)
, (5.18)
где 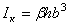 - момент инерции при кручении, аналог полярного момента инерции поперечного сечения бруса.
- момент инерции при кручении, аналог полярного момента инерции поперечного сечения бруса.
Коэффициенты  ,
, 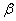 и
и  зависят от отношения сторон
зависят от отношения сторон 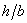 , и их значения приведены в табл. 4.1.
, и их значения приведены в табл. 4.1.
Таблица 4.1. Значения коэффициентов для прямоугольных сечений
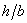
| 
| 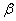
| 
|
| 1,0 | 0,208 | 0,140 | 1,0 |
| 1,2 | 0,219 | 0,166 | - |
| 1,4 | 0,228 | 0,187 | 0,865 |
| 1,6 | 0,234 | 0,204 | 0,845 |
| 1,8 | 0,240 | 0,217 | - |
| 2,0 | 0,246 | 0,229 | 0,796 |
| 2,5 | 0,258 | 0,249 | - |
| 3,0 | 0,267 | 0,263 | 0,753 |
| 4,0 | 0,282 | 0,281 | 0,745 |
| 6,0 | 0,299 | 0,299 | 0,743 |
| 8,0 | 0,307 | 0,307 | 0,743 |
| 10,0 | 0,313 | 0,313 | 0,743 |
| Более 10 | 0,333 | 0,333 | 0,743 |
Значения 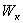 ,
,  и
и  для различных сечений приведены в табл.4.2.
для различных сечений приведены в табл.4.2.
Таблица 4.2. Геометрические характеристики жесткости и прочности для
некоторых сечений при кручении прямого бруса
| Форма поперечного сечения | Момент
инерции
при кручении

| Момент
сопротивления
при кручении
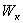
| Наибольшие
касательные
напряжения
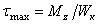
|
Квадрат
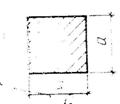
| 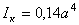
| 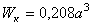
| В серединах сторон
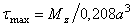 В углах
В углах 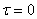
|
Круг с лыской
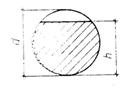
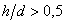
| 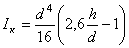
| 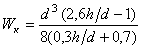
| В середине
плоского среза
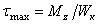
|
Эллипс
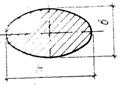
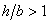
| 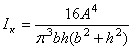
| 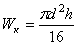
| В конце малой
полуоси
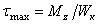 большой
большой
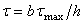
|
Равносторонний
треугольник
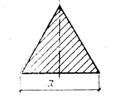
| 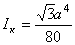
| 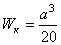
| В серединах сторон
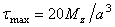 в углах
в углах 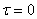
|
Правильный шести-
или восьмиугольник
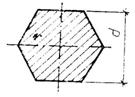
| 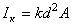 (для шестиугольника (для шестиугольника 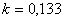 ,
для восьмиугольника ,
для восьмиугольника 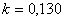 ) )
| 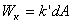 (для шестиугольника (для шестиугольника 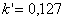 ,
для восьмиугольника ,
для восьмиугольника 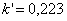 ) )
| В серединах сторон
 в углах
в углах 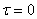
|
Форма клина
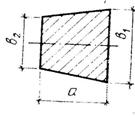
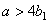
| 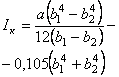
| 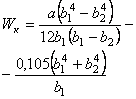
| В точках длинных сторон ближе к
широкому
основанию
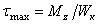
|
Полое эллиптическое
сечение
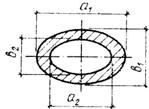
| 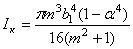 ; ;
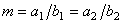 (
( 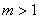 ); );
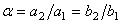 (
( 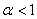 ) )
| 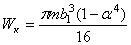
| В конце малой
полуоси
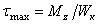 ,
большой ,
большой
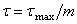 ,
при малой
толщине ,
при малой
толщине 
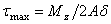 (равномерно по сечению) (равномерно по сечению)
|
Незамкнутое
кольцевое сечение
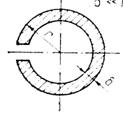
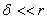
| 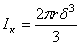
| 
| В точках
внутреннего и наружного сечения
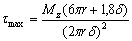
|
Дата добавления: 2015-08-08; просмотров: 1801;
