Решение. Найдем положение центра тяжести фигуры по формулам ;

Найдем положение центра тяжести фигуры по формулам 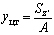; 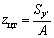. Разобьем фигуру на три простые: треугольник I, прямоугольник II и квадрант круга Ш. Площадь всей фигуры

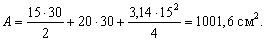
Для определения статических моментов выберем вспомогательные оси 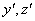, проходящие через центр тяжести прямоугольника II (рис. 2). Статический момент каждой фигуры равен площади фигуры, умноженной на координату центра тяжести этой фигуры в системе координат 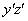. Суммарные статические моменты

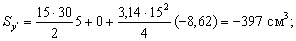
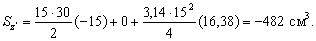
Координаты центра тяжести

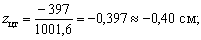
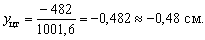
отложены на рис. 2.

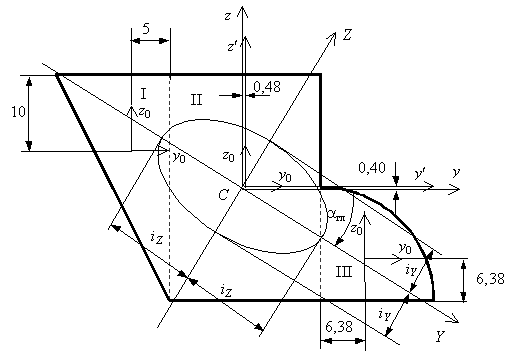
Рис.2

Проведем через центр тяжести центральные оси 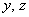(см. рис. 2) и найдем моменты инерции относительно этих осей, как сумму моментов инерций простых фигур, составляющих заданную фигуру. Для определения моментов инерции простых фигур I, II и Ш используем формулы 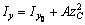, , 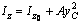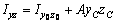. Моменты инерции относительно собственных осей 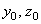прямоугольника, треугольника и квадранта круга вычисляем соответственно по формулам

; ; ,

; ; .

; .

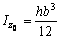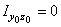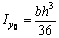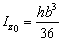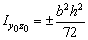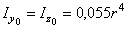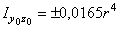Отсюда

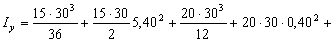
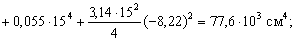
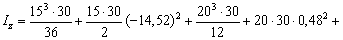
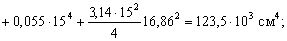
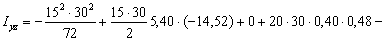
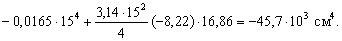
Теперь найдем положение главных осей инерции. Угол, на который надо повернуть ось 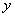, чтобы она стала главной осью, определяем по формуле :

;

; .

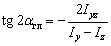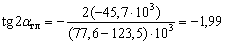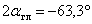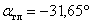В соответствии с правилом знаков откладываем отрицательный угол 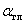по часовой стрелке и проводим главные центральные оси инерции Y, Z (см. рис. 2). Вычислим моменты инерции относительно этих осей по формуле :

; .

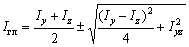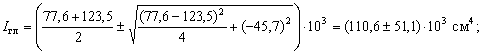
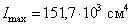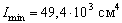Для проверки вычислений удобно использовать следующее свойство: сумма моментов инерций относительно двух любых пар ортогональных осей есть величина постоянная. Тогда должно быть

.

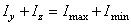В нашем примере .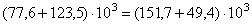

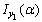Чтобы выяснить, какой момент инерции – максимальный или минимальный соответствует оси , исследуем знак второй производной функции по формуле .

.

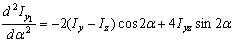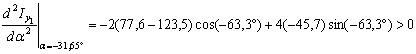Положительный знак второй производной означает, что оси соответствует минимальное значение момента инерции, т. е.

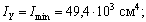
Найдем радиусы инерции относительно главных центральных осей по формуле 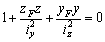и построим эллипс инерции.

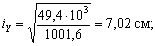
Эллипс инерции показан на рис. 2. Видно, что эллипс вытянут в том направлении, в котором вытянута фигура.