Решение. Усилия N1, и N2 в стержнях АА1, и ВВ1, шарнирно прикрепленных по концам, направлены вдоль осей этих стержней
Усилия N1, и N2 в стержнях АА1, и ВВ1, шарнирно прикрепленных по концам, направлены вдоль осей этих стержней. Реакция опоры К имеет горизонтальную составляющую НК, и вертикальную составляющую RК, т.к. эта опора препятствует горизонтальному и вертикальному перемещению точки К бруса.
Таким образом, всего имеется четыре неизвестные реакции (рис.2.54), а уравнений равновесия для плоской системы сил можно составить всего три. Следовательно, данная система один раз статически неопределима. Статически неопределимые системы рассчитывают путем совместного решения уравнений, полученных в результате рассмотрения статической, геометрической и физической сторон задачи.
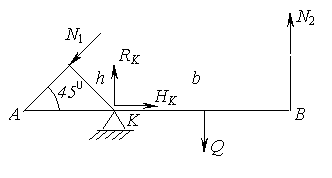
Рис. 2.54
1. Найдем усилия и напряжения в стержнях, выразив их через силу Q.
Статическая сторона задачи. По условию задачи необходимо определить усилия N1, и N2 стальных стержней АА1, и ВВ1, a в определений реакций НК, и RК нет необходимости. Поэтому достаточно из трех возможных уравнений равновесия использовать одно, в которое не входили бы реакция НК, и RК . Таким является уравнение в виде суммы моментов всех сил относительно шарнира К:
,
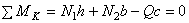где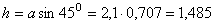 
м.
Подставляя в уравнение значения h, b, с, получим
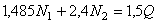. (а)
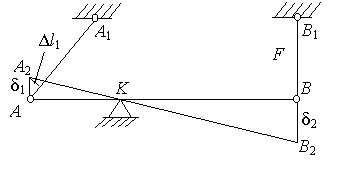
Рис.2.55
Геометрическая сторона задачи. Под действием внешней силы Q абсолютно жесткий брус повернется вокруг точки К. Шарниры А и В после деформации переходят в положение А2 и В2 соответственно, т.е. перемещаются по вертикали на величины 
и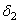 
(рис.2.55).
Из подобия треугольников AA2К и ВВ2К находим
. (b)
Выразим укорочение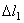 
стержня АА1 и удлинение 
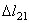стержня ВB1, через перемещения и .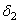
, 
,
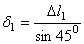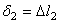откуда
или с учетом равенства (b)
(c)
Физическая сторона задачи. Используя закон Гука, записанный для абсолютных деформаций, выразим удлинения стержней через усилия
;
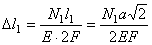; (d)
Подставим выражения (c) в условие (d)
,
после сокращения получим
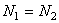(e)
Решаем совместно уравнения статики (a) и уравнение (e):
.
Определяем напряжения в стержнях 1 и 2:
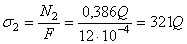Па,
Па.
2. Найдем допускаемую нагрузку [Q], приравняв большее из напряжений в двух стержнях допускаемому напряжению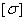 
= 160 МПа.
,
откуда
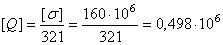Н.
3. Найдем предельную грузоподъемность системы Qпр. и допускаемую нагрузку [Qпр], если предел текучести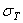 
= 240 МПа и запас прочности n = 1,5.
При увеличении нагрузки Q cверх значения [Q] напряжения в обоих стержнях сначала увеличивается прямо пропорционально нагрузке. При увеличении нагрузки до некоторой величины 
напряжение 
во второй стержне достигают предела текучести 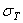, а усилие N2 - предельного значения N2пр = c1·F. При этом напряжение 
в первом стержне остается меньше 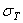. В процессе дальнейшего увеличения нагрузки напряжения во втором стержне остаются постоянными, равными пределу текучести, а в первом - возрастают, пока также не становятся равными 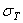, усилие N1 при этом равно 
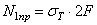. Это состояние системы называется предельным, соответствующим исчерпанию ее грузоподъемности. Дальнейшее, даже незначительное увеличение нагрузки связано с весьма большими деформациями системы. ВеличинуQ, вызываюшую предельное состояние, обозначают Qпр и называют предельной нагрузкой.
Для определения Qпр, подставим в уравнение (a) значения сил, соответствующих предельному состоянию, когда Q = Qпр, N1 = N1пр, N2 = N2пр:
,
откуда
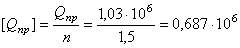Н.
Н.
4. Сравним величины допускаемых нагрузок [Q] и [Qпр]
.
Следовательно, при расчете на прочность данной системы по предельной нагрузке грузоподъемность ее увеличивается на 38%.
Дата добавления: 2015-08-08; просмотров: 1157;