Решение. Для решения задачи используем принцип независимости действия сил, а именно: отдельно построим эпюры продольных сил от действия сосредоточенной силы и от
Для решения задачи используем принцип независимости действия сил, а именно: отдельно построим эпюры продольных сил от действия сосредоточенной силы 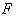 и от действия собственного веса, то есть от равномерно распределенной продольной нагрузки
и от действия собственного веса, то есть от равномерно распределенной продольной нагрузки 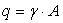 . Расчетная схема и эпюры продольных сил
. Расчетная схема и эпюры продольных сил 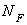 и
и 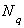 изображены на рис. 2.23.
изображены на рис. 2.23.
Полное удлинение стержня 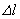 будет складываться из удлинения, полученного стержнем от действия сосредоточенной силы
будет складываться из удлинения, полученного стержнем от действия сосредоточенной силы 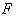 и от действия собственного веса:
и от действия собственного веса:
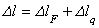 .
.
Или в другом виде:
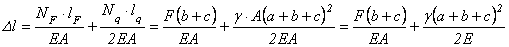 .
.
Для того, чтобы определить перемещение сечения m-n отбрасываем часть стержня ниже сечения m-n, а ее действие заменяем сосредоточенной силой 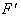 , равной продольной силе в сечении m-n:
, равной продольной силе в сечении m-n:
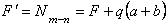 .
.
В результате получаем новую расчетную схему, которая приведена на рис. 2.24.
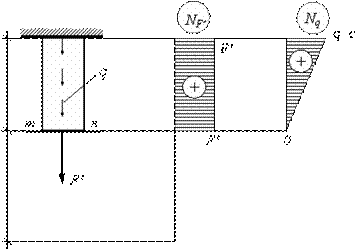
Рис.2.24.
А теперь решаем новую задачу о нахождении полного удлинения 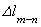 уже для данного стержня (рис. 2.23):
уже для данного стержня (рис. 2.23):
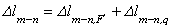 ,
,
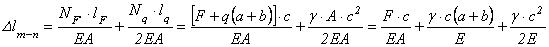 .
.
Расчет статически определимых стержневых систем
Статически определимая стержневая система – это система, в которой все неизвестные реакции опор и внутренние усилия можно определить из уравнений равновесия (статики).
Для «решения» любой стержневой системы необходимо выделить в ней объект равновесия. В связи с этим, все системы можно разделить на два типа:
1 тип – системы, состоящие из абсолютно жестких (недеформируемых) стержней и одиночных невесомых (деформируемых) стержней. Для стержневых систем этого типа объектами равновесия являются недеформируемые стержни.
2 тип – системы, состоящие из нескольких деформируемых стержней, соединенных в одной точке. Точки соединения двух и более стержней называются узлами, которые и являются объектами равновесия для систем 2-го типа.
Все соединения в элементах систем шарнирные, однако существуют определенные правила, по которым вводятся реакции и усилия в стержнях:
- в шарнире, соединяющем абсолютно жесткий элемент системы с «землей» или с другой конструкцией, всегда возникают две реакции – горизонтальная  и вертикальная
и вертикальная  ;
;
- в шарнире, соединяющем деформируемый стержень с абсолютно жестким стержнем или с другой конструкцией, всегда возникает одна реакция, направленная вдоль этого стержня и равная по величине усилию, возникающему в нем.
В абсолютно жестких стержнях никогда не возникает внутренних усилий, они не деформируются!
- в шарнире, соединяющем несколько деформируемых стержней (узловой шарнире), возникают усилия, направленные вдоль этих стержней и сходящиеся в этом узле.
Порядок решения большинства задач о проверке прочности статически определимых стержневых систем при расчете по допускаемым напряжениям сводится к следующим этапам:
1) находим внутренние усилия (продольную силу при растяжении-сжатии) и выявляем опасные сечения;
2) определяем напряжения;
3) после выявления максимальных напряжений используем условие прочности (формулы (2.26), (2.28), (2.32)) при растяжении-сжатии).
Дата добавления: 2015-08-08; просмотров: 718;
