ВОЛНОВАЯ функция

МАТЕМАТИЧЕСКИЕ ОСНОВЫ КВАНТОВОЙ МЕХАНИКИ

Квантовая механика микрочастицы, не ограниченная полуклассическим приближением, строится на математическом основании, использующем гильбертого пространство функций, то есть множество функций, для которых определено скалярное произведение в интегральной форме.

Основные положения

Состояние частицы описывается волновой функцией. Множество возможных состояний образует гильбертого пространство.

Волновая функция получается в результате решения уравнения Шредингера.

Физическая величина описывается оператором, действующим в гильбертовом пространстве.

Если состояние частицы является собственной функцией оператора, то есть функция восстанавливается при действии оператора, то результатом измерения величины является собственное значение оператора. Разложение волновой функции по ортонормированному базису собственных функций оператора дает вероятности возможных результатов измерения физической величины.

Квантовая механика в общем случае не дает однозначных результатов для поведения и характеристик частицы, но лишь вероятности этих результатов.

ВОЛНОВАЯ функция

Состояние частицы описывает комплексная волновая функция Y (пси), являющаяся амплитудой вероятности обнаружения частицы:

.

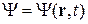Детектор частиц регистрирует 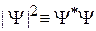. Физический смысл имеют:

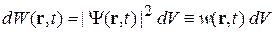
– вероятность обнаружения частицы в момент t в объеме 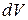около точки ;

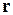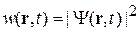
– плотность вероятности – вероятность обнаружения частицы в момент t в единичном объеме около точки r.

Выполняется нормировка вероятности

.

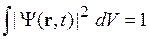Волновая функция:

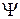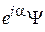1) Определена с точностью до постоянного фазового множителя. Состояния и , где 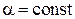, физически не различимы, поскольку ;

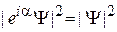2) Квадратично интегрируема, существует ;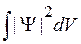

3) Удовлетворяет принципу суперпозиции. Если возможны состояния 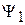и 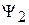, то возможно состояние

,

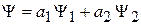где 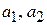– комплексные числа, определяющие вероятность обнаружения состояний 1 и 2.