И собственные значения

Собственная функция 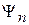оператора 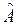определяется уравнением

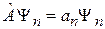, (2.8)

где 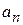– собственное значение оператора. Под действием оператора его собственная функция восстанавливается с точностью до постоянного множителя, который называется собственным значением.

Физический смысл собственного значения – если система находится в состоянии 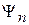, то измерение величины A, описываемой оператором 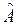, дает однозначный результат 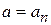. Собственные функции с разными собственными значениями взаимно ортогональны. Это исключает возможность получить при измерении неоднозначный результат.

Спектр оператора – это множество его собственных значений .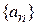

Если 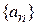счетное, то спектр дискретный.

Если 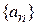образует непрерывный набор, то спектр непрерывный.

Если k разных собственных функций имеют одинаковые собственные значения, то спектр k-кратно вырожден.

Коммутирующие операторы имеют одинаковый набор собственных функций, соответствующие физические величины одновременно имеют определенные значения.

Доказательство:

Пусть 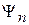– собственная функция 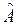, тогда

.

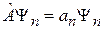Действуем оператором 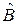на обе стороны равенства

.

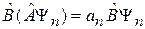Учитываем коммутативность операторов

,

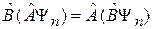получаем

.

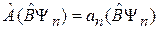Следовательно, 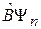– собственная функция 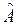, пропорциональная :

.

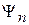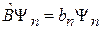Полученное равенство означает, что 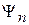– собственная функция 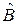с собственным значением .

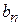Оператор координаты 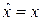. Пусть 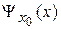– собственная функция с собственным значением 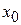, тогда

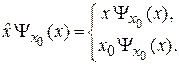
Верхнее равенство является определением оператора координаты, нижнее – определением собственной функции и собственного значения. В результате

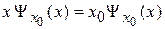
Сравниваем с фильтрующим свойством дельта-функции

,

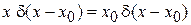находим

.

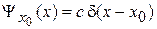Функция 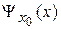равна нулю во всех точках, кроме 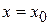, где x₀ – любое вещественное число, поэтому спектр x₀ непрерывный. Вид функции согласуется с физическим смыслом состояния – частица обнаруживается в точке x₀. В результате обоснована форма оператора координаты.

Как показано далее условие ортонормированности для непрерывного спектра имеет вид

.

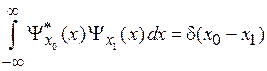Подстановка 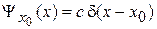дает

.

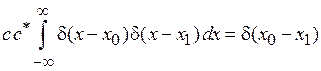Откуда 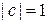, тогда собственная функция оператора координаты, или волновая функция частицы, находящейся в точке x₀, есть

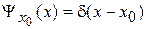. (2.9)

Оператор проекции импульса 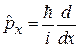. Уравнение на собственную функцию дает

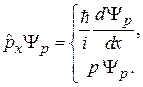
Получили дифференциальное уравнение первого порядка

.

Разделяем переменные

,

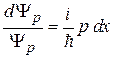интегрируем

,

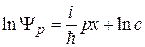находим

.

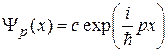Результат совпадает с координатной зависимостью плоской волны де Бройля

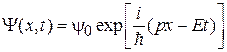, (1.11)

описывающей движение частицы с постоянным импульсом. В результате обоснована форма оператора импульса. Поскольку p – любое вещественное число, то спектр непрерывный. Условие ортонормированности для непрерывного спектра

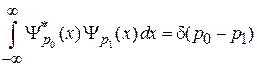
дает

.

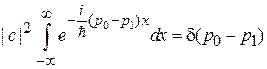Используя

,

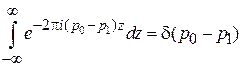находим 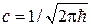. В результате собственная функция оператора импульса, или волновая функция частицы, движущейся с импульсом p, равна

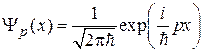. (2.10)