Основное уравнение лопастных насосов
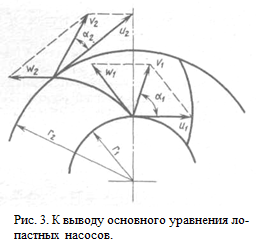 Рассмотрим процесс протекания жидкости по каналам рабочего колеса центробежного насоса (рис. 3). При этом сделаем два допущения:
Рассмотрим процесс протекания жидкости по каналам рабочего колеса центробежного насоса (рис. 3). При этом сделаем два допущения:
1) число лопаток рабочего колеса считается бесконечно большим;
2) жидкость проходит через каналы рабочего колеса в виде тождественных элементарных струек по одинаковым криволинейным траекториям, определяемым формой лопаток.
Движение жидкости является сложным. Каждая частичка жидкости, попадая на лопатку рабочего колеса, участвует одновременно в двух движениях: вращается вместе с колесом с переносной скоростью и1, равной окружной скорости вращения колеса; перемещается вдоль профиля лопаток с относительной скоростью w1. Вектор переносной скорости икасателен к окружности колеса, а вектор относительной скорости wкасателен к профилю лопатки.
Абсолютную скорость v1движения жидкости на входе в колесо можно определить из параллелограмма скоростей, используя теорему косинусов:
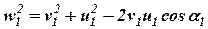 . (1)
. (1)
Аналогичное выражение получим из параллелограмма скоростей на выходе жидкости из колеса:
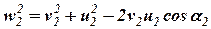 , (2)
, (2)
где a1 и a2 - углы между векторами абсолютной и окружной скоростей.
Составим уравнение Бернулли для двух сечений: в сечении 1, находящемся в непосредственной близости перед входом жидкости в колесо, и в сечении 2, расположенном после выхода жидкости с рабочего колеса. Пренебрегая потерями напора, получим:
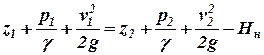 , (3)
, (3)
где z1 и z2 - координаты центра тяжести сечений 1 и 2; р1 и р2 - средние давления в этих сечениях; Нн — энергия, полученная жидкостью от рабочего колеса, равная полному напору, развиваемому насосом.
Запишем уравнение Бернулли для относительного движения жидкости по лопаткам в канале рабочего колеса, добавляя к числу действующих на жидкость массовых сил центробежную силу. Считаем, что работа центробежной силы начинается в сечении 1 после непосредственного поступления частиц жидкости на лопатки и заканчивается в сечении 2перед сходом с лопаток колеса:
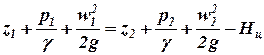 , (4)
, (4)
где Нц - удельная работа центробежной силы, т. е. работа, отнесенная к единице веса протекающей жидкости.
Определим работу центробежной силы Рпо перемещению частички жидкости массой тна расстоянии dr:центробежная сила P = mw2r; элементарная работа dA = mw2rdr.
Полная работа центробежной силы на пути от входа частицы жидкости на колесо с внутренним радиусом r1 до выхода с его внешней окружности радиусом r2определится интегрированием:
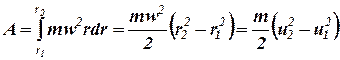 . (5)
. (5)
Разделив полученное выражение на единицу веса жидкости mg, получим удельную работу центробежной силы, отнесенную к 1 кг:
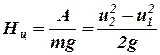 . (6)
. (6)
Подставив уравнение (6) в уравнение (4), получим:
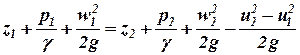 . (7)
. (7)
Вычтем из уравнения (3) уравнение (7):
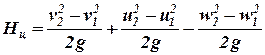 . (8)
. (8)
Заменим в уравнении (8) относительные скорости w1и w2, подставив их значения из уравнений (1) и (2). Тогда после преобразования получим уравнение для напора насоса:
Нн = (u2v2 cos a2 – u1v1 cos a1)/g. (9)
Это уравнение было выведено Л. Эйлером в 1755 г., т. е. раньше, чем центробежные насосы появились в производстве; оно называется основным уравнением лопастных машин.
Исходя из условий безударного входа жидкости в колесо, во избежание больших потерь напора при конструировании насосов стремятся к тому, чтобы направление вектора скорости подхода к колесу не отличалось от абсолютной скорости v1входа, а угол a был равен 90°. Тогда cos a1 = 0, а теоретический напор:
Нн = u2v2 cos a2 /g. (10)
Из уравнения (10) видно, что для получения максимальных значений напора угол a2 должен быть небольшим. На практике a2= 8-15°.
Действительный напор насоса будет несколько меньше, чем определяемый по уравнению (10), по следующим причинам: из-за гидравлических сопротивлений, встречаемых жидкостью в насосе; из-за неравномерности распределения скоростей в поперечном сечении каждого канала, так как число лопаток ограничено.
Эти потери напора можно учесть, вводя гидравлический коэффициент полезного действия hги коэффициент Кz, учитывающий форму и число лопаток: hг= 0,80-0,95, Кz= 0,75-0,85.
Таким образом, действительный напор центробежного насоса:
Ннд = u2v2 cos a2hг Кz /g. (11)
Анализ уравнения Л. Эйлера (11) позволяет сделать следующие выводы:
1. Напор центробежного насоса не зависит от рода жидкости и числа лопаток рабочего колеса.
2. Напор насоса будет тем больше, чем больше окружная скорость на внешней окружности рабочего колеса, пропорциональная его диаметру и частоте вращения.
3. Напор насоса будет увеличиваться по мере уменьшения угла между векторами окружной скорости колеса и абсолютной скорости схода жидкости.
Отметим, что основное уравнение Л. Эйлера справедливо не только для лопастных насосов, но и для гидравлических турбин, также представляющих собой лопастные машины, но с обратным процессом. Поэтому применительно к гидравлическим турбинам уравнение Л. Эйлера имеет вид:
Нн = (u1v1 cos a1 - u2v2 cos a2)/g. (12)
Дата добавления: 2015-07-10; просмотров: 1335;
