Механике. Преобразования Лоренца

А. Эйнштейн распространил механический принцип относительности Галилея на все без исключения физические явления (в том числе и оптические). Это означало, что скорость распространения света в вакууме в разных системах отсчета одинакова. Такое решение проблемы поиска абсолютной системы отсчета, относительно которой измерялись бы абсолютные скорости движения тел, было подготовлено исследованиями А. Пуанкаре, Х. Лоренца и
Д. Лармора, а также специальными экспериментами. Заслуга Эйнштейна состояла в том, что он давал объяснение уже известным фактам на основе нового представления о пространстве и времени.

Таким образом, А. Эйнштейн заложил основы специальной теории относительности, которая представляет собой, по существу, физическую теорию пространства и времени. В ней рассматриваются лишь инерциальные системы отсчета в отличие от общей теории относительности, в которой исследуются процессы в неинерциальных системах. Время в специальной теории относительности считается однородным, а пространство - однородным и изотропным. Теория относительности называется также релятивистской теорией, а рассматриваемые в ней специфические явления - релятивистскими эффектами.

Базируется специальная теория относительности на двух постулатах.

1. Принцип относительности: все физические явления (механические, электрические, оптические) в различных инерциальных системах отсчета протекают одинаковым образом, вследствие чего никакими опытами внутри системы отсчета невозможно установить, покоится она или движется прямолинейно и равномерно.

2.Принцип инвариантности скорости света: скорость света в вакууме не зависит от скорости движения источника или приемника света и одинакова во всех инерциальных системах отсчета.

В классической механике пространство и время рассматриваются независимо друг от друга. При этом считается, что время абсолютно и течет одинаково во всех инерциальных системах отсчета ( 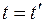). Это находится в противоречии с принципом постоянства скорости света в вакууме. Этому же принципу противоречит и теорема сложения скоростей в классической механике (17.8), полученная на основании преобразований Галилея. Действительно, если в системе 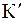распространяется световой сигнал со скоростью 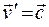, то в системе К его скорость 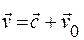. Согласно же второму постулату .

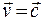Все это позволяет сделать вывод, что преобразования Галилея в теории относительности не выполняются и должны быть заменены другими формулами, которые включали бы в себя уравнения преобразования и пространственных координат и времени. Такие формулы впервые были получены на основе анализа уравнений Максвелла для электромагнитного поля Х. Лоренцем в 1899 г. и по предложению А. Пуанкаре называются преобразованиями Лоренца. Запишем эти преобразования для случая, когда система отсчета 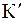движется относительно системы К вдоль оси X c постоянной скоростью v.

От преобразований Галилея преобразования Лоренца отличаются, во-первых, присутствием в уравнениях координат множителя

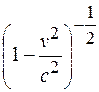
и, во-вторых, отличием времени в разных системах.

Более того, время в преобразованиях Лоренца связано с пространством (координатой х) и зависит от скорости движения системы, т. е. время является относительным.

При малых скоростях 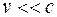значение величины 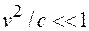и из формул (18.1), (18.2) находим:

Полученные уравнения совпадают с уравнениями (17.4) и (17.5) - преобразованиями Галилея. Следовательно, классическая механика является частным случаем теории относительности или релятивистской механики.

При 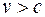выражения для х' и t' в преобразованиях Лоренца становятся мнимыми. Это находится в соответствии с тем, что осуществить движение со скоростью, большей скорости света в вакууме, невозможно. Нельзя также пользоваться системой отсчета, движущейся со скоростью с, так как при 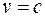в формулах для х', x и t, t' преобразований Лоренца в знаменателях получается ноль, и величины становятся неопределенными.