Релятивистский закон сложения скоростей
Получим закон сложения скоростей. Обозначим v - скорость движения системы 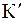 относительно системы К, u - скорость точки относительно системы
относительно системы К, u - скорость точки относительно системы 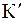 , w - скорость точки относительно системы
, w - скорость точки относительно системы 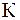 . Если движение происходит только вдоль осей Х и
. Если движение происходит только вдоль осей Х и 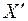 , то закон сложения скоростей получим следующим образом.
, то закон сложения скоростей получим следующим образом.
Запишем выражения скоростей:
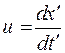 ,
, 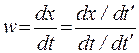 .
.
Продифференцируем преобразования (18.1) для величин x и t по времени t':
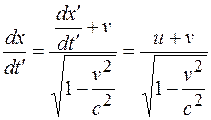 ;
; 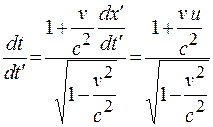 .
.
Подставим результаты в выражение для w и получим
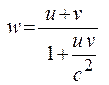 . (19.6)
. (19.6)
Формула (19.6) представляет собой закон сложения скоростей в релятивистской механике или релятивистский закон сложения скоростей. Если 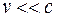 , он переходит в закон сложения скоростей классической механики. Покажем, что при сложении скоростей результат не превышает скорости света в вакууме. Пусть система
, он переходит в закон сложения скоростей классической механики. Покажем, что при сложении скоростей результат не превышает скорости света в вакууме. Пусть система 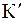 движется относительно системы К со скоростью
движется относительно системы К со скоростью 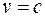 , а фотон движется относительно системы
, а фотон движется относительно системы 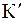 в том же направлении со скоростью
в том же направлении со скоростью 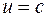 . Тогда на основании формулы (19.6) получаем, что и относительно системы К скорость фотона
. Тогда на основании формулы (19.6) получаем, что и относительно системы К скорость фотона 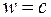 .
.
Дата добавления: 2015-08-08; просмотров: 980;
