Релятивистская динамика

В классической механике импульс определяется выражением

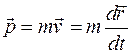, (20.1)

где 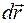- перемещение тела, а dt - промежуток времени в системе отсчета, относительно которой движется тело. Этот промежуток времени не является инвариантом, и, чтобы закон сохранения импульса был инвариантным по отношению к преобразованиям Лоренца, время движения должно быть измерено в собственной системе отсчета, в которой тело покоится. Промежуток собственного времени 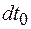является инвариантом.

Согласно вышесказанному, релятивистский импульс будет определяться выражением

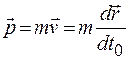. (20.2)

Так как dt и 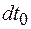в соответствии с формулой (19.5) связаны соотношением

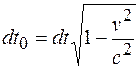, (20.3)

то, подставив выражение (20.3) в соотношение (20.2), получим

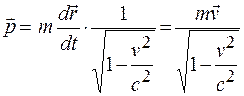. (20.4)

При 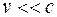выражение (20.4) переходит в выражение (20.1).

В классической физике справедливы две формулировки второго закона Ньютона (6.1) и (6.4). В релятивистской механике справедлива только вторая из них. Подставив в формулу (6.4) выражение (20.4), получим основное уравнение динамики материальной точки (частицы):

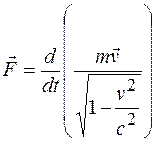. (20.5)

Отсюда следует, что в релятивистской механике сила не является инвариантом. Чтобы закон сохранения энергии был инвариантным по отношению к преобразованиям Лоренца, свободной частице, кроме кинетической энергии, нужно приписать дополнительную энергию, равную 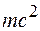. Тогда полная энергия частицы, равная сумме ее кинетической энергии и 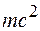, будет равна

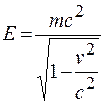. (20.6)

Из выражения (20.6) следует, что неподвижная частица обладает энергией

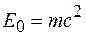, (20.7)

которая называется энергией покоя.

Заметим, что смысл понятия "полная энергия" в релятивистской механике иной, чем в классической. В релятивистской механике в полную энергию не входит потенциальная энергия частицы (энергия взаимодействия с другими телами). Соответственно, потенциальная энергия не будет входить и в энергию покоя.

Сопоставляя выражения (20.4) и (20.6), приходим к выводу, что полная энергия и импульс частицы связаны соотношением

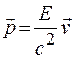. (20.8)

Исключив из выражений (20.4) и (20.6) скорость частицы v, получим соотношение

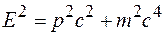, (20.9)

связывающее полную энергию и импульс частицы.

На его основе можно ввести новую трактовку массы, принятую в современной научной литературе: масса есть физическая величина, квадрат которой определяется выражением

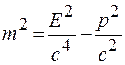. (20.10)

При переходе от одной инерциальной системы отсчета к другой энергия и импульс изменяются, а масса m остается неизменной, т. е. является инвариантом. Согласно современной терминологии понятия "релятивистская масса" и "масса покоя" являются устаревшими.

Массу можно также ввести, пользуясь выражением (20.7), как величину, равную частному от деления энергии покоя на квадрат скорости света, т. е.

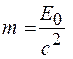. (20.11)

Из формулы (20.7) следует, что масса является мерой энергии тела в состоянии покоя.

В теории относительности масса - не аддитивная величина, а энергия и импульс - аддитивные величины. Действительно, так как суммарная энергия двух взаимодействующих частиц равна 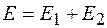, а импульс 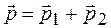, то согласно выражению (20.10) получим

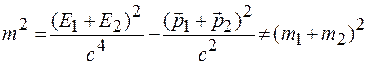. (20.12)

Это происходит вследствие того, что суммарная масса зависит от угла между векторами импульсов 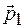и .

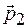Заметим, что в классической механике масса аддитивна.

Законы классической механики не допускают существования частиц с массой, равной нулю. Однако релятивистская механика не запрещает существование таких частиц. В соответствии с формулами (20.4) и (20.6) частица с массой 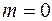может обладать определенным импульсом и энергией, но лишь при условии, что 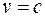(в этом случае выражения для импульса и полной энергии представляют собой неопределенность типа 0/0, которая может равняться конечному числу). Таким образом, частицы, не обладающие массой, могут существовать, только двигаясь со скоростью света. Связь между импульсом и полной энергией такой частицы в соответствии с формулой (20.9) определяется выражением

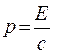. (20.13)

Примером безмассовой частицы является фотон.