Суперпозиция полей. Поле диполя

Если электрическое поле создается системой точечных зарядов, то напряженность такого поля в любой точке равна векторной сумме напряженностей полей, создаваемых в этой точке каждым зарядом в отдельности:

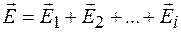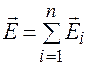или . (23.1)

Это утверждение является обобщением экспериментов и называется принципом суперпозиции (наложения) полей.

Воспользуемся принципом суперпозиции для расчета поля электрического диполя. Диполем называется система двух точечных зарядов, равных по абсолютной величине, противоположных по знаку, расстояние между которыми много меньше расстояния до тех точек, в которых рассматривается поле системы.

Вектор 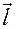, направленный от отрицательного заряда к положительному, называется плечом диполя (рис. 23.1). Величина, равная произведению значения заряда диполя на его плечо, называется электрическим моментом диполя:

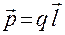. (23.2)

Направление вектора электрического момента совпадает с направ­лением плеча диполя. Единицей электрического момента является кулон-метр (Кл·м).

Определим напряженность электрического поля жесткого диполя (с неизменным значением плеча) на перпендикуляре, восстановленном из центра диполя к его оси (рис. 23.2).

По принципу суперпозиции полей находим

.

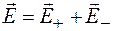Поскольку точки на перпендикуляре удалены от зарядов на одинаковые расстояния х и заряды имеют одинаковые значения, то

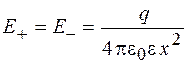. (23.3)

Из подобия треугольников следует, что

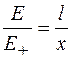. (23.4)

Объединяя выражения (23.3) и (23.4), находим

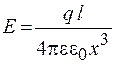. (23.5)

Выполним замену:

,

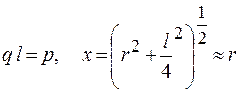так как .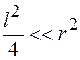

С учетом этого выражение (23.5) приводим к виду

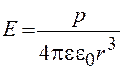. (23.6)

Можно доказать, что в произвольной точке поля напряженность определяется соотношением

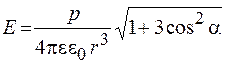, (23.7)

где 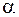- угол между плечом диполя и направлением на данную точку.

Из формулы (23.7) следует, что поле диполя не является сферически симметричным, значение напряженности определяется не зарядом q, а модулем электрического момента р и с увеличением расстояния в любом направлении убывает пропорционально .

Представление о диполе широко используется при изучении свойств диэлектриков, молекулы которых рассматриваются как жесткие или упругие диполи.