Принцип относительности Галилея

Рассмотрим две системы отсчета, движущиеся относительно друг друга с постоянной скоростью 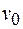(рис 17.1).

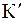Одну из этих систем (К) с координатными осями ХYZ будем условно считать неподвижной. Вторая система ( ) с осями 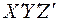движется относительно системы К равномерно и прямолинейно со скоростью 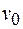. За направление движения выберем направление оси Х.

Скорость 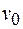называется переносной скоростью движения системы. Пусть в начальный момент времени начала координат (точки О и 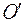) совпадают. Рассмотрим движение материальной точки М относительно систем координат К и 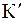в направлении оси Х (и 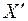также). Скорость v материальной точки в системе К называется абсолютной скоростью, в системе 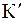скорость 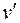– относительная скорость материальной точки.

Как следует из рисунка 17.1, в любой момент времени

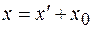, (17.1)

где х - координата материальной точки в системе К, 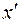- в системе 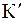, 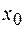- расстояние между началами координат систем 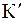и К.

Так как по условию система 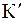движется равномерно и прямолинейно, то к моменту времени t

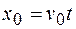. (17.2)

Из формул (17.1) и (17.2) получаем

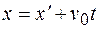. (17.3)

Кроме того, очевидно, что 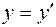и 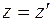. Учтем также принятое в классической механике предположение, что время в обеих системах отсчета течет одинаковым образом, т. е. 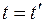. Тогда с учетом уравнения (17.3) получаем четыре уравнения:

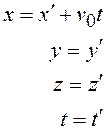(17.4)

Система уравнений (17.4), с помощью которых можно перейти от координат точки в подвижной системе 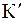к координатам в неподвижной системе К, называется прямыми преобразованиями Галилея. Обратные преобразования используются для перехода от системы К к системе :

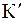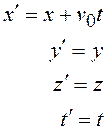(17.5)

Преобразования Галилея справедливы при скоростях, значительно меньших скорости света в вакууме.

Продифференцируем по времени соотношения (17.4):

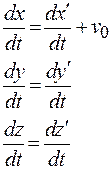(17.6)

В формулах (17.6) производные координат по времени представляют собой проекции скоростей материальной точки относительно систем К и 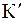. Поэтому соотношения (17.6) принимают следующий вид:

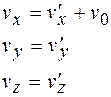(17.7)

Три скалярных соотношения (17.7) эквивалентны следующему соотношению векторов:

. (17.8)

Выражение (17.8) представляет собой теорему сложения скоростей в классической механике.

Продифференцируем по времени соотношение (17.8):

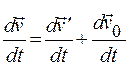, (17.9)

где 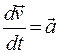- ускорение материальной точки в неподвижной системе К; 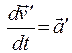- ускорение в подвижной системе 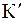, , 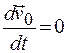так как .

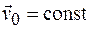Тогда из выражения (17.9) находим

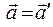. (17.10)

На основании формулы (17.10) заключаем, что ускорение материальной точки во всех системах отсчета, движущихся относительно друг друга прямолинейно и равномерно, одинаково. Поэтому если одна из этих систем инерциальная, то и остальные будут инерциальными.

Умножим левую и правую части равенства (17.10) на массу материальной точки m: 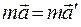, или

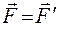. (17.11)

Это соотношение означает, что во всех инерциальных системах отсчета силы, действующие на материальную точку, будут одинаковы. Следовательно, уравнения динамики не изменяются при переходе от одной инерциальной системы отсчета к другой. В этом случае говорят, что уравнения динамики инвариантны по отношению к преобразованию координат, соответствующему переходу от одной инерциальной системы отсчета к другой. Следовательно, в классической механике уравнения динамики инвариантны по отношению к преобразованиям Галилея.

С механической точки зрения все инерциальные системы отсчета совершенно эквивалентны. Практически это проявляется в том, что никакими механическими опытами, проведенными в пределах данной системы, нельзя установить, находится она в состоянии покоя или в состоянии равномерного и прямолинейного движения.

Указанные обстоятельства были выяснены Галилеем и сформулированы в механическом принципе относительности, согласно которому все механические явления в различных инерциальных системах отсчета протекают одинаковым образом, вследствие чего никакими механическими опытами невозможно установить, покоится данная система отсчета или движется прямолинейно и равномерно. Сформулированный принцип носит название принципа относительности Галилея.

Если система 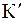движется с ускорением относительно инерциальной системы К, то она является неинерциальной системой. В этом случае в формуле (17.9) 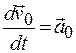- ускорение системы К' относительно системы К. Тогда из формулы (17.9) получаем 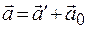. Умножив на массу все члены этого равенства, находим

.

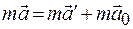Отсюда для движения в неинерциальной системе 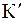имеем

.

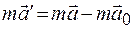В этой формуле 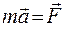- сила, приложенная к телу. Для расчета ускорения 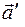тела относительно неинерциальной системы 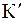необходимо знать величину 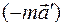. Она называется силой инерции и определяется произведением массы тела на ускорение системы, взятым со знаком "-": .

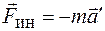Силу инерции в некотором смысле можно назвать фиктивной силой, так как она не связана с воздействием тел друг на друга.

Таким образом, уравнение второго закона Ньютона в неинерциальной системе отсчета будет иметь вид

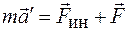. (17.12)

Введение сил инерции дает возможность описывать движение тел в любых (как инерциальных, так и неинерциальных) системах отсчета с помощью одних и тех же уравнений движения.