И вращательного движения

Энергией называется общая количественная мера различных форм движения материи. Для описания различных форм движения, изучаемых в физике, вводятся соответствующие им формы энергии – механическая, внутренняя, электромагнитная и др. В механике различают кинетическую энергию, обусловленную движением тела, потенциальную энергию, обусловленную положением тела в потенциальном поле сил, и полную энергию, равную сумме кинетической и потенциальной энергий. Механическая работа является мерой изменения механической энергии тела или системы тел.

Единица энергии - джоуль (Дж).

Получим выражение для кинетической энергии 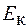при поступательном движении тела. Для этого выразим работу, совершенную некоторой силой при движении тела, через его скорость.

Элементарная работа равна

.

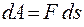Подставляя в эту формулу выражения силы и перемещения, получаем

.

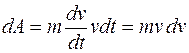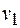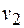Если на некотором конечном отрезке траектории скорость изменилась от до , то совершенная при этом работа равна

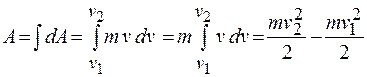. (14.1)

Совершенная при движении тела работа определяется изменением его кинетической энергии, т. е.

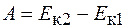. (14.2)

Сравнивая выражения (14.1) и (14.2), получаем формулу кинетической энергии тела массой m, движущегося со скоростью v:

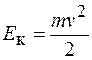. (14.3)

Умножив на m числитель и знаменатель правой части равенства (14.3) и зная, что произведение mv равно импульсу тела р, для кинетической энергии получаем выражение

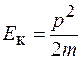. (14.4)

Рассчитаем теперь кинетическую энергию вращающегося тела. Выберем в теле элемент объема - материальную точку массой dm, движущуюся по окружности радиусом r с линейной скоростью v,и найдем ее кинетическую энергию на основании формулы (14.3):

.

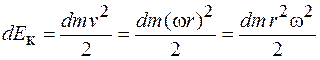Произведение 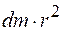представляет собой момент инерции материальной точки 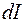. Следовательно,

.

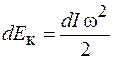Для нахождения кинетической энергии твердого тела необходимо вычислить сумму энергий всех его элементов. Учитывая, что угловые скорости движения всех точек тела одинаковы, находим

.

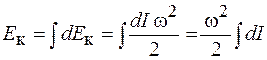Так как 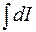определяет момент инерции всего твердого тела I, относительно оси вращения, то получаем

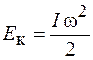. (14.5)

Полученное выражение (14.5) аналогично формуле (14.3) для кинетической энергии тела, движущегося поступательно. При вращательном движении мерой инертности служит момент инерции, а быстрота движения характеризуется угловой скоростью.

В случае произвольного движения тела его кинетическая энергия будет складываться из энергии поступательного движения со скоростью, равной скорости центра масс 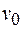, и энергии вращения вокруг оси, проходящей через центр масс тела, т. е.

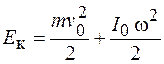. (14.6)