Работа при поступательном и вращательном движении
Пусть тело под действием силы F перемещается за некоторый промежуток времени на расстояние ds (рис. 13.1). При этом вектор 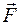 с направлением перемещения
с направлением перемещения 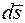 составляет угол
составляет угол 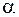 . Работой в механике называют величину, равную произведению модуля вектора силы на модуль вектора перемещения и на косинус угла между этими векторами.
. Работой в механике называют величину, равную произведению модуля вектора силы на модуль вектора перемещения и на косинус угла между этими векторами.
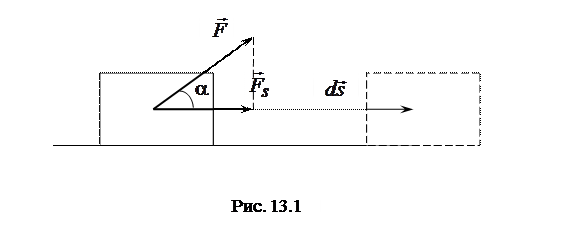
Для элементарной работы имеем
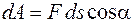 . (13.1)
. (13.1)
Из рисунка 13.1 следует, что
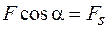 , (13.2)
, (13.2)
где 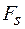 – проекция вектора силы на направление перемещения. Объединяя выражения (13.1) и (13.2), получаем
– проекция вектора силы на направление перемещения. Объединяя выражения (13.1) и (13.2), получаем
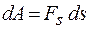 . (13.3)
. (13.3)
Работа – скалярная величина. Если направление вектора силы с направлением перемещения образует острый угол (  ), то
), то 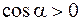 и
и 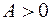 . Если угол
. Если угол 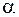 – тупой (
– тупой ( 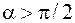 ), то
), то 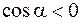 и
и 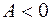 . При
. При 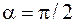 работа
работа 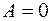 .
.
Единица работы - джоуль (Дж). За один джоуль принимается работа, совершенная силой в один ньютон при перемещении тела на один метр в направлении действия силы.
Если при перемещении значение силы и ее направление на отрезке пути 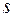 не изменяются, работа определяется выражением
не изменяются, работа определяется выражением
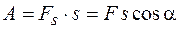 . (13.4)
. (13.4)
Работа переменной силы на некотором пути может быть вычислена как сумма бесконечно большого числа элементарных работ:
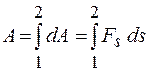 . (13.5)
. (13.5)
В этой формуле должна быть известна зависимость силы от положения тела в пространстве на всем участке траектории движения от положения 1 до положения 2.
На практике важно не только значение совершенной работы, но и время, в течение которого она совершается. Работа, совершенная за единицу времени, называется мощностью. Если работа dА совершена за время dt, то мощность равна
 . (13.6)
. (13.6)
Если мощность не меняется с течением времени, то она определяется выражением
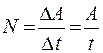 . (13.7)
. (13.7)
Единица работы – ватт (Вт). Из формулы (13.6) или (13.7) следует, что один ватт – это мощность, при которой за каждую секунду совершается работа, равная одному джоулю.
Подставляя выражение (13.4) в уравнение (13.6), получим
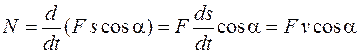 ;
;
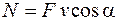 . (13.8)
. (13.8)
Мощность равна произведению модуля вектора силы на модуль вектора скорости и на косинус угла между ними.
Найдем работу, которую совершают внешние силы при повороте тела вокруг неподвижной оси (рис. 13.2).
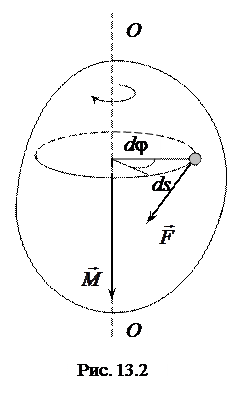 Пусть к некоторой точке тела приложена сила
Пусть к некоторой точке тела приложена сила 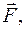 вызывающая вращение точки по окружности радиусом r. За некоторое время dt радиус-вектор точки повернется на угол dj, а точка переместится по дуге окружности на расстояние
вызывающая вращение точки по окружности радиусом r. За некоторое время dt радиус-вектор точки повернется на угол dj, а точка переместится по дуге окружности на расстояние
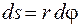 .
.
При движении материальной точки силой F совершена работа
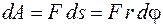 .
.
Так как 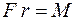 – момент силы относительно оси вращения, то для работы получаем выражение
– момент силы относительно оси вращения, то для работы получаем выражение
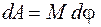 . (13.9)
. (13.9)
Эта формула применима для твердого тела при условии, что М - момент всех сил, действующих на тело. Полная работа при вращении тела
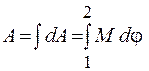 . (13.10)
. (13.10)
Дата добавления: 2015-08-08; просмотров: 2258;
