Основное уравнение динамики вращательного движения

Пусть твердое тело с моментом инерции I вращается вокруг оси ОО с угловым ускорением b (рис. 10.1). Выберем в этом теле бесконечно малый элемент объема, в котором сосредоточена масса dm. Этот элемент можно рассматривать как материальную точку, движущуюся по окружности радиусом r с тангенциальным ускорением 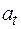. По второму закону Ньютона, на точку действует сила

.

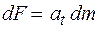Поскольку 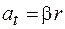, то .

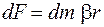Левую и правую части этого равенства умножим на r:

. (10.1)

В полученной формуле 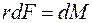- момент силы, приложенный к элементу твердого тела, 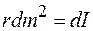– момент инерции этого элемента.

Тогда выражение (10.1) принимает вид

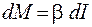. (10.2)

Поскольку моменты сил, действующих на разные элементы твердого тела, направлены по оси вращения в одну сторону, а угловое ускорение всех элементов одинаково, то для нахождения результирующего момента сил требуется определить алгебраическую сумму бесконечно большого числа бесконечно малых величин dM - проинтегрировать выражение (10.2):

.

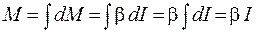Таким образом, получаем

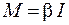, (10.3)

или в векторной форме

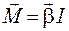. (10.4)

Выражения (10.3) и (10.4) называют основным уравнением (основным законом) динамики вращательного движения.

Так как 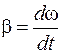, а 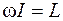, то основное уравнение динамики вращательного движения можно преобразовать следующим образом:

,

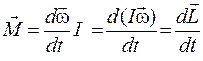т. е.

. (10.5)

Момент силы (пары сил) равен производной момента импульса тела по времени. Это другая формулировка основного закона динамики вращательного движения.

Уравнения (10.4) и (10.5) аналогичны уравнениям второго закона Ньютона для поступательного движения (формулы (6.1) и (6.4)). Поэтому аналогию величин и уравнений поступательного и вращательного движения можно продолжить и для динамики вращательного движения (табл. 2).

Таблица 2