Законы сохранения импульса и момента импульса

Рассмотрим систему, состоящую из N материальных тел. Эти тела могут взаимодействовать как между собой, так и с телами, не принадлежащими данной системе. В соответствии с этим силы, действующие на тела системы, можно разделить на внутренние и внешние. Внутренними называют силы, с которыми на данное тело воздействуют остальные тела системы, внешними - силы, обусловленные воздействием тел, не принадлежащих системе. Если внешние силы отсутствуют или компенсируют друг друга, система называется замкнутой (изолированной).

Импульсом системы называется векторная сумма импульсов тел, образующих систему:

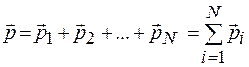, (12.1)

где 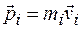- импульс i-го тела системы.

К системе тел применим второй закон Ньютона (6.4) и найдем сумму действующих сил:

,

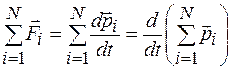где 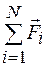- результирующая всех сил, приложенных к телам системы.

Внутренние силы всегда возникают парами, равны по модулю и противоположны по направлению - их векторная сумма равна нулю. Для замкнутой системы по определению равна нулю и сумма внешних сил. Тогда получаем:

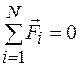и .

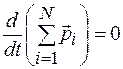Отсюда следует:

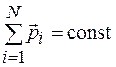. (12.3)

Формула (12.3) является математическим выражением закона сохранения импульса, согласно которому импульс изолированной системы тел не изменяется при любых взаимодействиях, происходящих внутри системы. На законе сохранения импульса основан принцип действия реактивных двигателей.

Воспользуемся основным законом динамики вращательного движения (10.5) для системы тел:

,

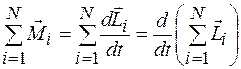где 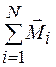- сумма моментов сил, действующих в системе. Для замкнутой системы она равна нулю 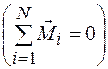, значит,

.

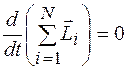Отсюда следует, что

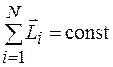. (12.4)

Поскольку 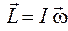, то на основании формулы (12.4) получаем

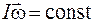. (12.5)

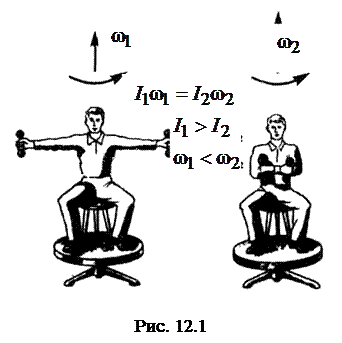Формулы (12.4) и (12.5) - математические выражения закона сохранения момента импульса, согласно которому момент импульса системы тел остается постоянным, если момент сил, действующих на эту систему, равен нулю.