Закон сохранения энергии в механике. В общем случае тело может обладать одновременно и кинетической, и потенциальной энергиями

В общем случае тело может обладать одновременно и кинетической, и потенциальной энергиями. Сумма этих энергий образует полную механическую энергию

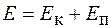. (16.1)

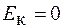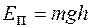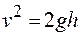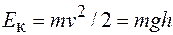При перемещении тела потенциальная и кинетическая энергии могут превращаться друг в друга. Рассмотрим случай свободного падения покоившегося тела с высоты h. До начала падения , . В конце падения и , при этом 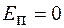. Следовательно, потенциальная энергия полностью превращается в кинетическую. Полная энергия при этом остается неизменной.

Полная механическая энергия системы, состоящей из N тел, между которыми действуют консервативные силы, складывается из потенциальной энергии системы как целого и из суммарной кинетической энергии тел, образующих систему:

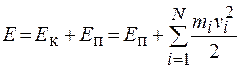. (16.2)

Если в консервативной системе из N тел изменяется их взаимное положение, то за счет изменения потенциальной энергии этих тел будет совершена работа

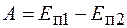. (16.3)

Если система замкнута, то эта работа идет на изменение кинетической энергии тел, образующих систему, т. е.

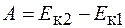. (16.4)

Из формул (16.3) и (16.4) находим

.

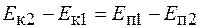Отсюда получаем

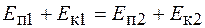
или

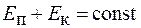. (16.5)

Формула (16.5) является математическим выражением закона сохранения энергии, согласно которому полная механическая энергия замкнутой, консервативной системы тел остается величиной постоянной.

Между законами динамики и законами сохранения существует принципиальная разница.

Законы динамики однозначно определяют характер движения. На основании этих законов можно найти (по крайней мере, теоретически) положение тел в процессе движения.

Законы сохранения говорят о том, какие процессы запрещены и потому в природе не происходят. Законы сохранения проявляются как принципы запрета: любое явление, при котором не выполняется хотя бы один из законов сохранения, запрещено. Всякое явление, при котором не происходит нарушения ни одного из законов сохранения, в принципе может происходить.

Своим происхождением законы сохранения обязаны свойствам симметрии пространства и времени. Было доказано, что из однородности пространства вытекает закон сохранения импульса, из изотропности пространства - закон сохранения момента импульса, из однородности времени - закон сохранения энергии.