Комплекс
Исходя из приведенных положений Лэнгмюр получил уравнение адсорбции, которое имеет вид:
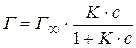 (гиперболическая функция)
(гиперболическая функция)
где 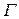 - величина адсорбции;
- величина адсорбции;
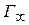 - емкость адсорбционного монослоя, или число адсорбционных центров, приходящихся на единице площади поверхности или на единицу массы адсорбента.
- емкость адсорбционного монослоя, или число адсорбционных центров, приходящихся на единице площади поверхности или на единицу массы адсорбента.
Для сорбции газов и паров, уравнение Лэнгмюра имеет вид:
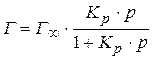 .
.
|
 Типичный вид изотермы адсорбции Лэнгмюра показан на рис. 7.2.
Типичный вид изотермы адсорбции Лэнгмюра показан на рис. 7.2.

Рис. 7.2. Изотерма адсорбции Лэнгмюра.
Уравнение Лэнгмюра преобразуется в уравнение прямой:
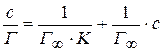
Такая зависимость позволяет графически определить оба постоянных параметра адсорбционной изотермы. На рис. 7.3 представлена типичная изотерма адсорбции в линейных координатах. Экстраполяция зависимости до оси ординат дает отрезок равный 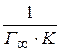 , а тангенс угла наклона прямой равен
, а тангенс угла наклона прямой равен 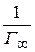 .
.

Рис. 7.3. Изотерма адсорбции Лэнгмюра в прямолинейных координатах.
Изотерма адсорбции может иметь ступенчатый вид:


Рис. 7.4. Изотерма ступенчатой адсорбции
Изотерма адсорбции Фрейндлиха (1880-1941гг., немецкий физико-химик).
Представления Лэнгмюра идеализируют и упрощают действительную картину адсорбции. В действительности поверхность большинства адсорбентов неоднородна и адсорбция не ограничивается образованием мономолекулярного слоя, вследствие чего уравнение адсорбции усложняется.
Фрейндлих предположил, что адсорбция зависит от давления и концентрации и предложил эмпирическое уравнение, которое имеет вид степенной функции:
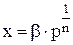 или
или 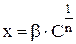 ,
,
где 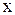 - масса адсорбированного вещества, п
- масса адсорбированного вещества, п
иходящаяся на 1 г адсорбирующего материала, г.;
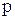 - давление;
- давление;
 - концентрация;
- концентрация;
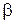 и
и 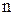 - константы, которые не имеют физического смысла и играют роль подгоночных коэффициентов. Для большинства случаев
- константы, которые не имеют физического смысла и играют роль подгоночных коэффициентов. Для большинства случаев 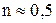 .
.
В логарифмической форме уравнение имеет вид:
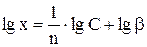 ,
,
т.е. сорбция выражается линейной зависимостью. Наклон прямой прямо пропорционален 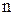 , на оси ординат отсекается отрезок, равный
, на оси ординат отсекается отрезок, равный 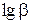 .
.
Позже Зельдович теоретически вывел уравнение, эмпирически предложенное Фрейндлихом.

Рис. 7.5. Изотермы адсорбции Фрейндлиха.
Дата добавления: 2015-08-08; просмотров: 1228;
