Построение изотермы адсорбции и нахождение величин .
Изотерма адсорбции описывается уравнением Ленгмюра:
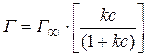
где 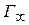 – предельная концентрация вещества, адсорбиро-
– предельная концентрация вещества, адсорбиро-
ванного на 1 м2 поверхности, кмоль/м2;
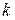 - константа равновесия, равная отношению констант скоростей процессов десорбции и адсорбции.
- константа равновесия, равная отношению констант скоростей процессов десорбции и адсорбции.
Зная Г можно рассчитать площадь S, приходящуюся на 1 молекулу.
Число адсорбированных молекул на 1 м2 составляет:
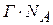
Отсюда:

С увеличением Г величина S уменьшается и при 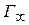 достигает минимального значения
достигает минимального значения 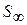 :
:
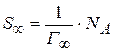
Пользуясь 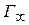 вычисляют толщину
вычисляют толщину 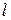 насыщенного поверхностного слоя:
насыщенного поверхностного слоя:
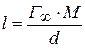
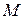 - молекулярная масса;
- молекулярная масса;
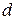 - плотность адсорбированного вещества.
- плотность адсорбированного вещества.
Строят изотерму ПН (зависимость  от концентрации ПАВ).
от концентрации ПАВ).
По изотерме ПН рассчитывают Г по уравнению Гиббса.
Для этого к кривой  в нескольких точках проводят касательные до пересечения их с осью ординат, проводя также параллельные прямые до пересечения с осью ординат (рис. 6.5). Из треугольника АВD находят
в нескольких точках проводят касательные до пересечения их с осью ординат, проводя также параллельные прямые до пересечения с осью ординат (рис. 6.5). Из треугольника АВD находят 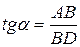 или
или 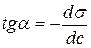 . Находят несколько значений
. Находят несколько значений 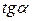 для C1, C2, C3,…и строят зависимость
для C1, C2, C3,…и строят зависимость  .
.
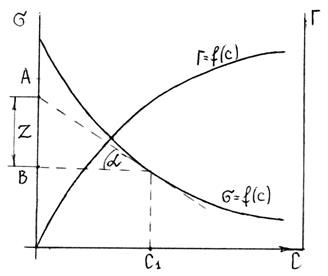
Рис. 6.5. Построение изотермы адсорбции по изотерме
поверхностного натяжения.
Каждой концентрации С соответствует отрезок Z на оси ординат.
Длина отрезка, выраженная в единицах ПН равна: 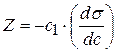 , так как согласно построению
, так как согласно построению 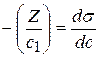 .
.
Подставив полученные значения Z в уравнение:
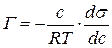
получим:
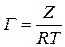
Используя Z для ряда концентраций, рассчитывают адсорбцию Г.
Строят изотерму адсорбции, откладывая по оси абсцисс С, а по оси ординат Г.
Где сложно провести касательную (в интервале концентраций 0,2-0,15 моль/л) рассчитывают изменение: 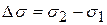 и
и 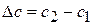 и определяют
и определяют 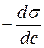 для средней концентрации 0,1.
для средней концентрации 0,1.
Данные заносят в таблицу:
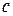
| 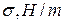
| 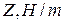
| 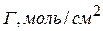
| 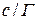
|
Значение 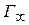 определяют графически по уравнению Лэнгмюра, преобразовав его в уравнение прямой линии (рис. 6.6):
определяют графически по уравнению Лэнгмюра, преобразовав его в уравнение прямой линии (рис. 6.6):
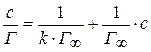
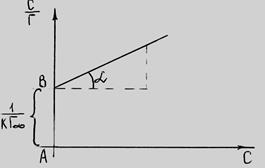
Рис. 6.6. График уравнения Ленгмюра в прямолинейных координатах.
Угол 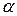 на рис. 6.6 позволяет определить
на рис. 6.6 позволяет определить 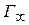 :
: 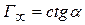 .
.
Отрезок 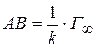 .
.
Из этого уравнения определяем 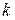 .
.
Из уравнения  вычисляем
вычисляем 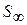 и
и 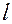 из уравнения
из уравнения 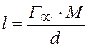 .
.
Дата добавления: 2015-08-08; просмотров: 3271;
