Перевод дробных чисел

Если при переводе конечной дроби в другую систему счисления получается конечная дробь, то такой перевод называется точным. Если при переводе получается бесконечная дробь, тогда перевод называется приближенным.

Перевод дробных чисел из n-й в десятичную систему счисления - вещественное число переводится из n-й в десятичную систему счисления с использованием формализованного представления числа.

Перевод дробных чисел с нулевой целой частью из десятичной в n-ую систему счисления - дробное число X, у которого целая часть равна 0, переводится из десятичной в n-ую систему счисления по следующему алгоритму:

1) умножить X на n;

2) получить цифру как целую часть числа X и приписать ее справа от имеющихся цифр;

3) обнулить целую часть числа X;

4) выполнять шаги 1-3, пока X ¹ 0 (при точном переводе) или до получения нужного количества цифр в дробной части (при приближенном переводе с заданной точностью).

Пример. Перевести число 0,6875 в двоичную систему счисления.

Решение. Вновь схему перевода запишем в виде столбца.

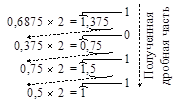
На последнем шаге перевода получена единица. После обнуления целой части получим 0. Значит, перевод закончен. Результат перевода числа 0,6875 в двоичную систему счисления – число 0,1011₂.

Если бы нам было необходимо получить дробную часть с точностью до 3 знаков, то процесс перевода был бы остановлен после получения 3 цифр в дробной части. □

Перевод дробных чисел с ненулевой целой частью из десятичной в n-ую систему счисления - при переводе дробных чисел из десятичной в n-ую систему счисления отдельно переводятся целая и дробная части.

Десятичная система счисления может использоваться в качестве промежуточного этапа при переводе чисел из одной системы счисления в другую. Приведенные в этой главе правила позволяют перевести числа из одной системы счисления в десятичную, а из нее – в любую другую системы счисления.