Второй закон термодинамики. - возможность самопроизвольного протекания реакции;

План:

- возможность самопроизвольного протекания реакции;

- энтропия;

- изобарно - изотермический потенциал или свободная энергия Гиббса.

Самопроизвольными называются процессы, в результате которых может быть получена полезная работа 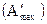, несамопроизвольными называются процессы, на которые нужно затратить работу.

Рассмотрим два самопроизвольных процесса – растворение гидроксида натрия и растворение нитрата аммония:

;

.

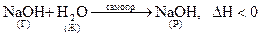Это самопроизвольные процессы, но один из них сопровождается выделением тепла, а другой – поглощением тепла. Как видим, знак теплового эффекта процесса (энтальпийный фактор) не определяет однозначно возможность самопроизвольного протекания процесса. Существует 2-ой фактор самопроизвольности процесса - энтропийный фактор.

Что же такое энтропия?

Состояние любой системы может быть описано, с одной стороны, по значению измеряемых параметров системы (макросостояний системы), с другой стороны, состояние системы можно описать множеством мгновенных микросостояний, которым соответствуют разные энергетические уровни микрочастиц, составляющих нашу систему.

Число микросостояний, которое соответствует данному макросостоянию вещества, называется термодинамической вероятностью его состояния (W), т. е. W – это число способов, которыми молекулы можно распределить по разным энергетическим уровням.

С термодинамической вероятностью состояния связана функция состояния системы, называемая энтропией(S) .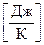

S = k ln W, где k – постоянная Больцмана, k ≈ 1,38∙10^-23 Дж/K ,

W – термодинамическая вероятность состояния системы.

Для 1 моль вещества:

S = R ln W, где R – универсальная газовая постоянная, здесь S измеряется в .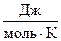

Вероятность состояния максимальна при максимальной разупорядоченности системы, т. е. энтропия максимальна тогда, когда система находится в наиболее разупорядоченном состоянии. Именно к этому система стремится самопроизвольно.

Любая система стремится перейти в состояние наибольшего беспорядка, т. е. самопроизвольно, любая система стремится к увеличению энтропии. И энтропияявляется мерой беспорядка в системе. Она увеличивается в таких физических процессах, как плавление, кипение, расширение газов. В химических процессах энтропия увеличивается, если из исходных веществ, взятых в твёрдом или жидком состояниях, получается газообразные продукты реакции, или - если число молекул в ходе реакции увеличивается.

Пример:

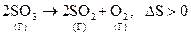, т. е. энтропия растёт, т. к. увеличивается количество движущихся частиц.

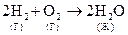, DS < 0 , - энтропия уменьшается т. к. уменьшается количество частиц (из 3-х в 2) и система переходит из газообразного состояния в жидкое.

Рассмотрим изменение энтропии в системе при переходе из одного, состояния, характеризуемого объёмом V₁ в другое – с объёмом V₂:

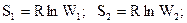
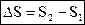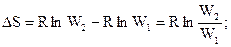
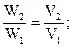, Þ ;

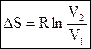Если V₂ > V₁, то DS > 0, если V₂ < V₁, то DS < 0, т.е. при увеличении объема энтропия увеличивается.

Энтропия идеального кристалла при абсолютном нуле равна нулю, поэтому можно рассчитать абсолютное значение энтропии для каждого вещества. В таблицах приводится стандартное значение энтропии (S°) 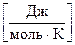при стандартных условиях.

Энтропия – функция состояния вещества, значит, не зависит от пути перехода системы из одного состояния в другое. Для обратимых изотермических процессов (фазовых переходов), изменение энтропии равно изменению энтальпии, деленному на температуру:

.

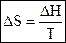Энтропия зависит от температуры:

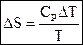, где С_Р – молярная теплоёмкость при постоянном давлении.

Функция, которая связывает и энтальпийный и энтропийный фактор, G – свободная энергия Гиббса, или изобарно – изотермический потенциал.

G = H - T×S, где Н – энтальпия, Т – абсолютная температура, S – энтропия.

Для изобарно-изотермических процессов:

DG = DH - TDS, т. е. в изменении свободной энергии Гиббса учитывается и энтальпийный и энтропийный факторы.

Если система совершает полезную работу, то её энергия убывает.

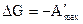, где 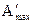- полезная работа.

DG < 0, (1) – для самопроизвольных процессов.

DG = 0, (2) – в состоянии равновесия.

Уравнения (1) и (2) – математическая запись 2-го закона термодинамики.