Механика. Материальная точка. Движение материальной точки. Скорость и ускорение произвольно движущейся точки
Механика – это наука о механическом движении тел и происходящих при этом взаимодействиях между ними. Кинематика – раздел механики, который рассматривает лишь само перемещение тел в зависимости от времени.
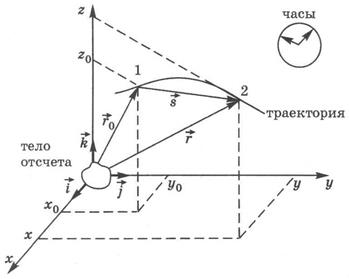
|
 ,проведенного из начала координат в рассматриваемую точку (для точек 1 и 2 на рис. 1.1 это векторы
,проведенного из начала координат в рассматриваемую точку (для точек 1 и 2 на рис. 1.1 это векторы 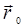 и
и 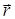 ), либо с помощью координат x, у, z– проекций вектора
), либо с помощью координат x, у, z– проекций вектора 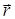 на координатные оси:
на координатные оси:
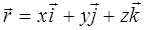 , (1.1)
, (1.1)
где 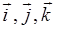 - векторы, указывающиенаправление осей Ox, Oy, Oz и равные по модулю единице.
- векторы, указывающиенаправление осей Ox, Oy, Oz и равные по модулю единице.
Вектор 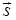 ,соединяющий начальное и конечное положение тела (точки 1 и 2 на рис. 1.1), называют перемещением. Модуль перемещения меньше или равен пути l– расстоянию, пройденному телом по траектории; они равны в случае прямолинейного движения в одну сторону.
,соединяющий начальное и конечное положение тела (точки 1 и 2 на рис. 1.1), называют перемещением. Модуль перемещения меньше или равен пути l– расстоянию, пройденному телом по траектории; они равны в случае прямолинейного движения в одну сторону.
Для определения быстроты движения тела вводят понятие мгновенной скорости 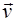 тела в данной точке траектории, равную первой производной от радиус-вектора
тела в данной точке траектории, равную первой производной от радиус-вектора 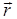 (или перемещения
(или перемещения 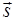 ) по времени t:
) по времени t:
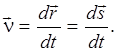 (1.2)
(1.2)

Вектор 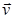 в каждой точке траектории пространства направлен по касательной к ней (рис. 1.2).
в каждой точке траектории пространства направлен по касательной к ней (рис. 1.2).
Часто используют понятие средняя путевая скорость 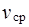 – скалярная физическая величина, равная отношению пути l, пройденного телом за времяt, к этому времени t.
– скалярная физическая величина, равная отношению пути l, пройденного телом за времяt, к этому времени t.
|
Быстроту изменения скорости определяют, введя понятиемгновенного ускорения 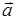 – ускорения в данной точке траектории, равного первой производной от скорости
– ускорения в данной точке траектории, равного первой производной от скорости 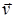 по времени t:
по времени t:
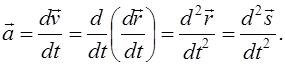 (1.3)
(1.3)
Проекцию вектора ускорения 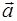 на направление касательной к траектории называют касательным (тангенциальным) ускорением
на направление касательной к траектории называют касательным (тангенциальным) ускорением 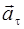 , а на направление, перпендикулярное к касательной, – нормальным (центростремительным) ускорением
, а на направление, перпендикулярное к касательной, – нормальным (центростремительным) ускорением 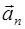 (см. рис. 1.2):
(см. рис. 1.2):
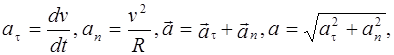 (1.4)
(1.4)
где v– числовое значение скорости; R– радиус кривизны траектории в данной ее точке, он равен радиусу окружности R, вписанный в малый участок траектории вблизи этой точки.
Касательное ускорение характеризует изменение скорости тела по ее числовой величине (по модулю скорости), а нормальное ускорение – по направлению.
Приведем вывод формул для ускорений aτ и an . Для этого возьмем на траектории движения две близко расположенные точки 1 и 2, разделенные интервалом времени ∆t(рис. 1.3).
|
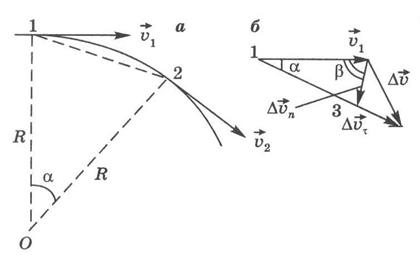
Перенесем вектор  параллельно самому себе в точку 1 и, отложив на нем отрезок, равный по модулю вектору
параллельно самому себе в точку 1 и, отложив на нем отрезок, равный по модулю вектору  , получим точку 3 (рис. 1.3б). Тогда вектор
, получим точку 3 (рис. 1.3б). Тогда вектор  можно представить в виде суммы двух векторов
можно представить в виде суммы двух векторов 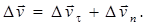 При ∆t→0 углы α и β стремятся соответственно к 00 и 900, поэтому вектор
При ∆t→0 углы α и β стремятся соответственно к 00 и 900, поэтому вектор 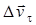 , направленный по касательной к траектории, будет характеризовать изменение числового значения скорости, а вектор
, направленный по касательной к траектории, будет характеризовать изменение числового значения скорости, а вектор 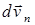 будет перпендикулярен к
будет перпендикулярен к 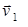 . Следовательно,
. Следовательно,
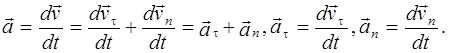 (1.5)
(1.5)
Длина дуги и расстояние по прямой между точками 1 и 2 (рис. 1.3а) при малых ∆t→dtбудут равны dl1,2 = ds1,2 = vdt. Из подобия треугольников ∆102 (рис. 1.3а) и ∆1v13 (рис. 1.3б) следует
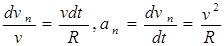 .
.
Дата добавления: 2015-08-08; просмотров: 1274;
