Кинематика вращательного движения

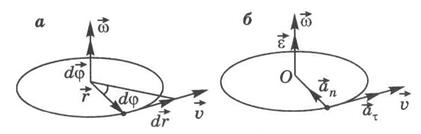
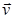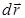Пусть м. т. движется со скоростью по окружности радиуса rвокруг неподвижной оси вращения (рис.1.4а). Положение точки на окружности определяет радиус-вектор , а вектор его элементарного приращения направлен по касательной к окружности. Введем понятие вектора элементарного углового перемещения 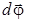: он равен по модулю углу элементарного поворота dφ, направлен по оси вращения и связан с направлением вращения правилом правого буравчика, а именно: направление вращения буравчика должно совпадать с направлением вращения материальной точки, тогда поступательное движение буравчика определяет направление вектора 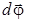(рис. 1.4а).

Быстроту вращения м. т. характеризует угловая скорость , равная первой производной от вектора углового перемещения по времени t:

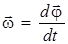(1.6)

Направление вектора угловой скорости 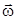и вектора элементарного углового перемещения 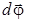совпадают.

Быстроту изменения угловой скорости характеризует вектор углового ускорения 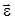, равный первой производной от угловой скорости 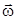по времени t:

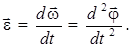(1.7)

Кроме перечисленных выше величин, для описания вращательного движения тела используют частоту вращения n, определяемую как число оборотов, совершенных телом за единицу времени, и период обращения Т,как время одного полного оборота. Справедлива следующая взаимосвязь ω, nи Т:

ω = 2πn= 2π/Т. (1.8)

Установим взаимосвязь линейных( 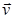, 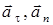) и угловых ( 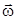, 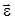) характеристик при вращательном движении.

Пользуясь определением векторного произведения двух векторов (см. Прил. 1) и рис. 1.4а, можно записать

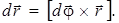(1.9)

Выражение (1.9) позволяет получить следующие формулы взаимосвязи линейных и угловых характеристик:

1) для скоросте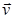й и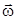

; v= ωr. (1.10)

2) для ускорений , ,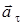

;

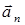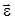
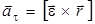; a_{τ =} εr , (1.11)

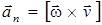, a_n = ων =ν²/r= ω²r. (1.12)