Поле бесконечной равномерно заряженной плоскости. Поле плоского конденсатора

Пусть электрическое поле создаётся зарядом, равномерно распределённым по поверхности безграничной плоскости, с поверхностной плотностью s (рис. 2.8.)

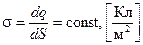
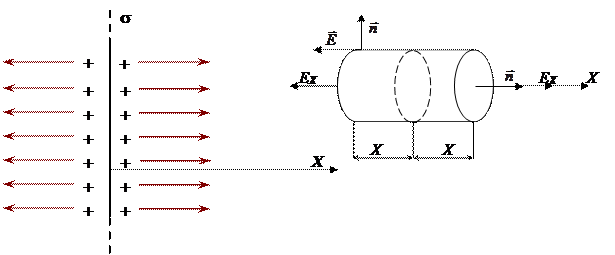
Рис. 2.8.

Из симметрии задачи следует, что поле повсюду направлено перпендикулярно к поверхности. Выясним, как меняется напряжённость поля по мере удаления от заряженной плоскости.

В качестве гауссовой поверхности удобно выбрать цилиндр. Ось цилиндра направим перпендикулярно плоскости, его основание расположим на расстоянии Х симметрично по обе стороны от поверхности.

Вычислим поток вектора напряжённости через боковую поверхность и основания цилиндра. Как следует из рис. 2.8., поток вектора напряжённости 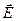через боковую поверхность цилиндра равен нулю, так как здесь повсюду векторы напряжённости «скользят» по поверхности и .

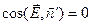Тогда полный поток через замкнутую цилиндрическую поверхность можно записать как поток через два основания цилиндра.

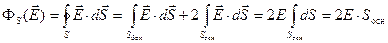(2.14)

Это величина, рассчитанная по определению потока.

Теперь воспользуемся теоремой Гаусса, заметив, что заряд q, «находящийся внутри гауссовой поверхности», в данном случае сосредоточен на площадке S = S_осн, «вырезанной» цилиндром на бесконечной плоскости

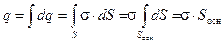(2.15)

Объединим результаты(2.15) и (2.14) в уравнение Гаусса:

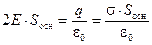
Откуда следует

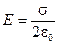(2.16)

Вывод. Поле, созданное бесконечной равномерно заряженной плоскостью, однородно. Оно не меняется с расстоянием от заряженной поверхности ни по величине, ни по направлению.

Теперь рассмотрим еще один важный пример. Пусть поле создаётся двумя бесконечными плоскостями, заряженными разноименно, но с одинаковой по величине поверхностной плотностью заряда (рис. 2.9.). Это важная идеализация электростатики — плоский конденсатор. Каждая обкладка этого конденсатора создаёт однородное поле, напряжённость которого мы только что установили (2.16):

.

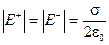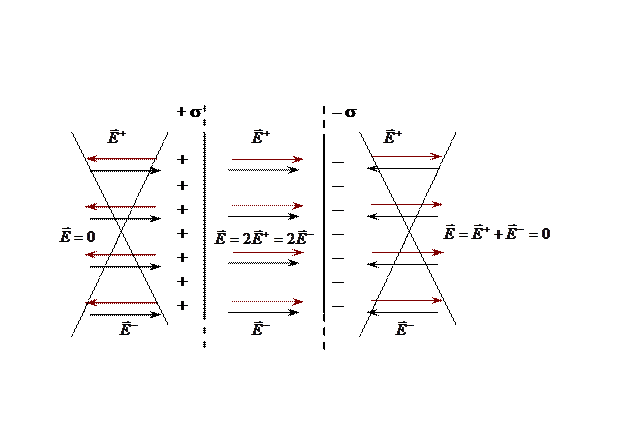
Рис. 2.9.

Силовые линии поля положительно заряженной плоскости направлены от неё, а отрицательной — к плоскости. При сложении этих полей, напряжённость результирующего поля вне конденсатора оказывается равной нулю, а внутри конденсатора, где эти поля совпадают по направлению, — поле удваивается:

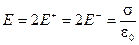. (2.17)