Работа сил электростатического поля при перемещении заряда. Потенциал и разность потенциалов.

Рассмотрим произвольное перемещение (1–а–2) заряда q в электростатическом поле. Пусть поле создаётся неподвижным точечным зарядом Q (рис. 3.1.). В процессе перемещения на заряд q действует кулоновская сила:

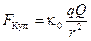. (3.1)

Рис. 3.1.

Её работа на перемещении 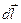равна:

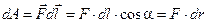. (3.2)

Здесь dr = dlсosa — толщина сферической оболочки, окружающей заряд Q. Полная работа электрической силы равна сумме работ на всех участках траектории:

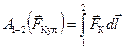. (3.3)

Теперь несложно показать, что эта работа не зависит от формы траектории и остаётся неизменной, если начальная и конечная точки траектории не меняют своего положения. Рассмотрим, например, перемещение того же заряда q из начальной точки 1 в конечную 2 по новой траектории 1–b–2. При преодолении прежнего сферического слоя на перемещении 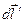электрическая сила совершит работу:

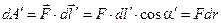. (3.4)

Но ведь эта работа в точности совпадает с работой на перемещении dl (3.2) по первоначальной траектории 1–а–2.

Полная работа, равная сумме элементарных работ на всех участках новой траектории, будет равна работе электрической силы на траектории 1–а–2:

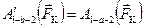. (3.5)

Вспомним, что силы, работа которых не зависит от вида траектории и определяется только положением её начальной и конечной точек, называются консервативными.

Мы пришли к выводу, что кулоновская сила консервативна. Впрочем, ничего неожиданного в этом выводе нет: ведь сила взаимодействия двух точечных зарядов может быть отнесена к классу центральных сил, а все центральные силы, как было установлено в механике, консервативны.

Итак, вычислим работу кулоновской силы при перемещении заряда q из точки 1 в положение 2 (по любой траектории):

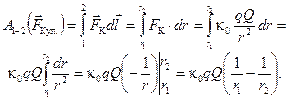(3.6)

Как и следовало ожидать, величина работы никак не связана с видом траектории. Она зависит только от положения её начальной (r₁) и конечной (r₂) точек.

В механике было показано, что работа консервативной силы равна убыли потенциальной энергии системы:

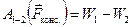. (3.7)

Присмотримся внимательнее к результату (3.6):

.

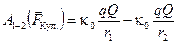Сопоставив этот результат с теоремой о работе консервативной силы (3.7), запишем уравнение:

,

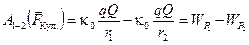из которого следует, что потенциальная энергия системы:

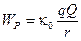+ const. (3.9)

Это потенциальная энергия системы двух точечных зарядов, или, что то же самое, энергия заряда q в электрическом поле точечного заряда Q.

Константа в выражении (3.9) принимается обычно равной нулю. Это означает, что принимается равной нулю энергия взаимодействия зарядов q и Q на бесконечном удалении их друг от друга (при r = ∞).Тогда на расстоянии r энергия взаимодействия равна 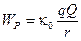. (3.10)

Потенциальная энергия заряженной частицы в электрическом поле зависит, таким образом, от величины заряда q и от его положения в поле относительно заряда Q, создающего поле.

Энергия единичного (q = 1) точечного заряда уже не будет связана с величиной этого пробного заряда q и может быть принята в качестве энергетической характеристики данной точки электростатического поля:

.

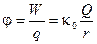Эта энергетическая характеристика поля получила название потенциал — j.

Потенциал произвольной точки электростатического поля равен энергии единичного положительного заряда, помещённого в эту точку.

Можно придать потенциалу и иной физический смысл.

Поместим заряд q в поле точечного заряда Q. Первоначально расстояние между зарядами — r. Отпустим заряд q. Под действием электрической силы отталкивания заряд q удалится в бесконечность (рис. 3.2.). На этом перемещении кулоновская сила совершит работу:

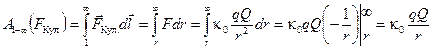. (3.11)

Эта работа не зависит от формы траектории, поэтому мы её вычислили, считая, что заряд q удаляется по радиусу.

Рис. 3.2.

Сравнивая (3.10) и (3.11), заключаем, что:

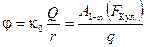. (3.12)

Потенциал некоторой точки электростатического поля равен работе, совершаемой электрической силой при эвакуации единичного положительного заряда из этой точки в бесконечность.

Теперь вычислим потенциал поля, созданного системой точечных зарядов Q₁, Q₂, …, Q_N.

При перемещении заряда q из точки 1 в бесконечность электрическая сила совершит работу, равную алгебраической сумме работ сил, действующих на движущийся заряд со стороны зарядов Q₁, Q₂, …, Q_N (рис. 3.3.):

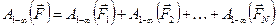
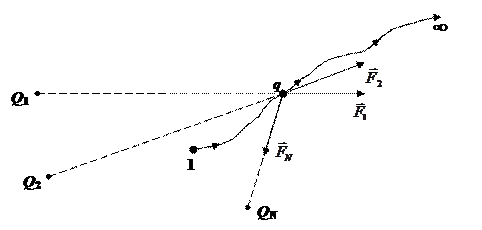
Рис. 3.3.

Согласно (3.12) работа каждой силы равна:

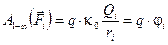. (3.13)

Здесь — потенциал поля, создаваемого в точке 1 зарядом Q_i.

Таким образом, суммарная работа равна:

,

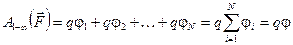где .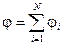

Потенциал поля, созданного системой точечных зарядов, равен алгебраической сумме потенциалов, создаваемых в рассматриваемой точке каждым из зарядов в отдельности:

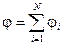. (3.14)

Результат (3.14) известен как «принцип суперпозиции для потенциала». Это очень важный вывод, позволяющий использовать понятие потенциала не только для характеристики полей точечных зарядов, но и для любых произвольных электростатических полей.

Ещё раз обратимся к вычислению работы электрической силы при перемещении заряда q из точки 1 теперь уже произвольного электростатического поля в бесконечность. Поскольку эта работа не зависит от формы траектории, унося заряд в бесконечность, пройдём предварительно точку 2 электростатического поля (рис. 3.4.).

Рис. 3.4.

Ясно, что вся работа на этом перемещении складывается из двух частей:

.

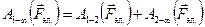Разделив это равенство на величину переносимого заряда q, получим:

,

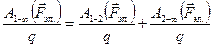или:

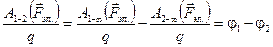. (3.15)

Здесь 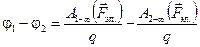— разность потенциалов двух точек поля. Она равна работе, совершаемой электрической силой при перемещении единичного заряда из первой точки во вторую:

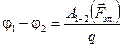. (3.16)

Таким образом, зная разность потенциалов двух точек поля, легко вычислить работу электрического поля, совершаемую при перемещении заряда q между этими точками:

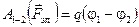. (3.17)

В международной системе единиц СИ потенциал (и разность потенциалов) измеряется в вольтах:

.

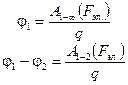
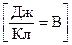Разность потенциалов двух точек электростатического поля равна одному вольту, если при переносе заряда q = 1Кл между этими точками, электрическая сила совершает работу А(F_эл.) = 1 Дж.

5.4. Теорема о циркуляции в вектора напряжённости электростатического поля

Существуют два равнозначных определения консервативной силы. Оба они подробно обсуждались в механике.

Консервативной называется сила, работа которой не зависит от формы траектории.

Консервативной называется сила, работа которой на замкнутой траектории равна нулю.

Рассмотрим перемещение заряда q в электростатическом поле по замкнутой траектории (рис. 3.5.). Заряд из точки 1 перемещается по пути L₁ в точку 2, а затем возвращается в исходное положение по другому пути L₂. В процессе этого движения на заряд со стороны поля действует консервативная электрическая сила:

.

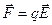Работа этой силы на замкнутой траектории L = L₁ + L₂ равна нулю:

.

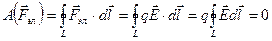Это уравнение, упростив, запишем так:

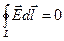. (3.18)

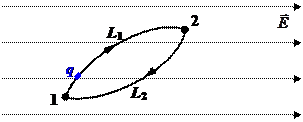
Рис. 3.5.

Разберём подробно последнее уравнение. Подынтегральное выражение — элементарная работа электрической силы, действующей на единичный положительный заряд, на перемещении 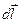(рис. 3.6.):

, (3.19)

здесь q = 1 — единичный заряд.

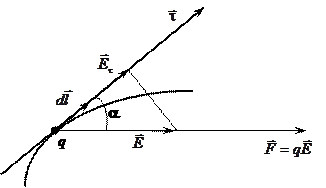
Рис. 3.6.

При подсчёте работы на замкнутой траектории необходимо сложить элементарные работы электрической силы на всех участках траектории. Иными словами, проинтегрировать (3.19) по замкнутому контуру L:

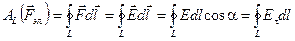. (3.20)

Интеграл по замкнутому контуру 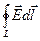= 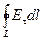называется циркуляцией вектора напряжённости электростатического поля по контуру L. По своей сути циркуляция вектора напряжённости — это работа электростатического поля, совершаемая при перемещении по замкнутому контуру единичного положительного заряда.

Так как речь идёт о работе консервативной силы, то на замкнутой траектории она равна нулю:

.

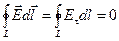Теорема о циркуляции в электростатике: циркуляция вектора напряжённости электростатического поля по любому замкнутому контуру равна нулю.

5.5. Связь напряжённости и потенциала электростатического поля

Потенциал и напряжённость — две локальные характеристики электростатического поля. То есть, это две характеристики — энергетическая и силовая — одной и той же точки поля.

Разумно предположить, что между ними должна существовать однозначная связь.

Для отыскания этой связи, вычислим работу электрической силы на элементарном перемещении dl заряда q в электростатическом поле 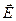(рис. 3.7.).

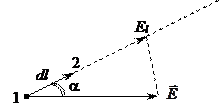
Рис. 3.7.

С одной стороны:

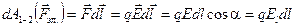. (3.21)

Но с другой стороны, эту же работу можно связать с разностью потенциалов (j₁ – j₂) = –(j₂ – j₁) = –dj:

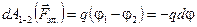. (3.22)

Объединив (3.21) и (3.22), получим:

E_ldl = –dj.

Или:

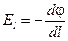. (3.23)

Важно отметить, что здесь E_l — проекция вектора напряжённости поля 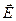на направление перемещения, а 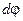— изменение потенциала при переходе в поле из точки 1 в точку 2.

Записав (3.23) для направлений x, y и z, получим соответствующие составляющие (проекции) вектора напряжённости:

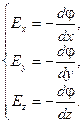(3.24)

Первое уравнение этой системы означает, что проекция вектора напряжённости на ось x равна частной производной потенциала по x, взятой с противоположным знаком.

Полный вектор напряжённости можно, как обычно, представить в виде векторной суммы:

.

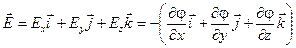Последнее уравнение принято записывать так:

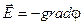. (3.25)

Здесь векторный оператор «градиент» grad = .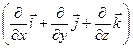

Уравнение (3.25) устанавливает искомую связь двух характеристик электростатического поля — напряжённости и потенциала: напряжённость электростатического поля равна градиенту потенциала с обратным знаком.

До последнего времени мы измеряли напряжённость поля в :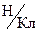

.

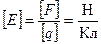Теперь, руководствуясь соотношением (3.23) можно получить ещё одну единицу измерения напряжённости:

.

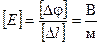Несложно показать, что эти две единицы измерения легко превращаются одна в другую:

.

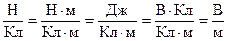5.6. Примеры расчёта потенциала электростатических полей

Установив связь двух характеристик электростатического поля — потенциала и напряжённости, покажем, как это соотношение можно использовать для расчёта потенциала.

Потенциал поля точечного заряда (рис. 3.8.)

Напряжённость поля точечного заряда Q известна в любой точке пространства:

.

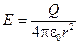Так как это сферически симметричное поле, его потенциал будет меняться только как функция r. Поэтому связь напряжённости и потенциала можно упростить и записать так:

.

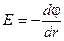Или:

.

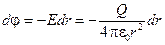Разность потенциалов двух точек поля:

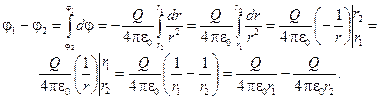
Полученный результат позволяет сделать два вывода:

1. Потенциал произвольной точки поля точечного заряда обратно пропорционален расстоянию от заряда до рассматриваемой точки:

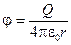. (3.26)

2. Потенциал бесконечно удалённой точки (r₂ ® ¥) равен нулю j_¥ = 0.

Множество точек одинакового потенциала образует в пространстве сферические эквипотенциальные поверхности.

Разность потенциалов на обкладках сферического конденсатора (рис. 3.9.)

Если обкладкам конденсатора сообщены заряды (+q) и (–q) , то между обкладками существует поле 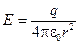(см. 2.19 ).

Воспользовавшись соотношением между напряжённостью и потенциалом электростатического поля, вычислим разность потенциалов между обкладками конденсатора:

;

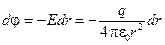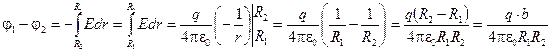(3.27)

Здесь b = (R₂ – R₁) — расстояние между обкладками конденсатора.

Лекция 4 «Электростатика проводников»

План лекции.

Электростатическое поле заряженного проводника.

Проводники во внешнем электрическом поле. Явление электростатической индукции. Электростатическая защита.

Электроёмкость проводника. Конденсаторы. Ёмкость конденсаторов.

Ёмкость плоского конденсатора.

Ёмкость сферического конденсатора.

Ёмкость цилиндрического конденсатора.

Энергия электрического поля. Плотность энергии электрического поля.

До сих пор мы изучали электрическое поле в пустоте — в вакууме. Как изменятся свойства поля, если пространство окажется заполненным веществом?

Все вещества по их отношению к электрическому полю принято делить на проводники и изоляторы — диэлектрики. Это деление довольно условное, потому что все вещества в большей или меньшей степени проводят электрический ток. Однако диэлектрики проводят ток хуже чем проводники не в 2 – 3 раза, а на 15 – 20 порядков, то есть электрическое сопротивление диэлектриков в 10¹⁵ ¸ 10²⁰ раз выше сопротивления проводников…

Влиянию проводников и изоляторов на электрические поля мы посвятим эту и следующую лекции.