Основы теории теплового подобия

7.2.1. Подобные процессы теплоотдачи

Теория теплового подобия – это система понятий и правил, обеспечивающих возможность переноса результатов экспериментов по определению коэффициентов теплоотдачи с одних объектов на другие.

Первые понятия о подобии даются в геометрии. В случае подобия двух треугольников каждая сторона большего треугольника превосходит сходственную сторону меньшего треугольника в определенное число раз. Это число называют к о н с т а н т о й п о д о б и я. Могут быть подобными и физические процессы.

Процессы конвективного теплообмена, протекающие в различных системах, при вполне определенных условиях могут быть подобны. Эти условия теплового подобия формулируются в виде трех правил [4].

1.Подобные процессы должны быть качественно одинаковыми, т.е должны иметь одинаковую физическую природу и описываться одинаковыми дифференциальными уравнениями. Так, например, процессы нагрева воды в закрытом сосуде и нагрева движущейся воды по трубе не могут считаться подобными, так как описываются различными дифференциальными уравнениями.

2.Условия однозначности подобных процессов должны быть одинаковы во всем, кроме численных значений постоянных, содержащихся в этих условиях.

3.Одноименные критерии подобных процессов должны иметь одинаковую численную величину.

Третье правило требует дополнительных разъяснений. Пусть в двух системах процессы конвективного теплообмена будут подобны. Запишем дифференциальные уравнения теплоотдачи для этих процессов с соответствующими индексами:

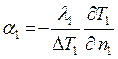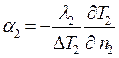и (7.5)

Введем константы подобия одноименных величин:

K_α = α₂/α₁; K_λ = λ₂/λ₁; K_т = Т₂/Т₁; K_l = n₂/n₁ = l₂/l₁,

где l - характерный геометрический размер системы.

Выразим величины второй системы через константы подобия и одноименные величины первой системы:

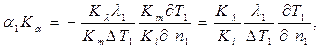
или

(7.6)

Уравнения (7.5) и (7.6) тождественны, так как они выражают связь между параметрами процесса, обусловленную дифференциальным уравнением теплоотдачи для одной и той же системы. Из условий тождественности уравнений следует, что

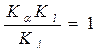(7.7)

Равенство (7.7) накладывает ограничение на выбор констант для подобных явлений: определенная их комбинация должна быть равна единице.

Подставив в выражение (7.7) значения констант подобия, будем иметь:

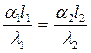(7.8)

Получили безразмерный комплекс величин, который для двух подобных систем имеет численно одинаковое значение. Этот безразмерный комплекс в честь немецкого ученого В. Нуссельта назван критериемНуссельта.

Таким образом, третье правило дает возможность распространить подобие на множество процессов теплообмена, отличающихся друг от друга величинами c, λ, ρ, c_p, l и т.д., но имеющих численно одинаковые их комбинации.

Переход от обычных физических величин к критериям подобия, которые составлены из тех же величин, но в других сочетаниях, создает важные преимущества. Прежде всего, достигается уменьшение числа независимых переменных, участвующих в формулировке решения рассматриваемой задачи. Это позволяет систему дифференциальных уравнений, описывающих теплообмен, заменить функциональной связью между критериями подобия. Кроме того, значения критериев подобия могут быть получены как результат множества различных комбинаций величин. Следовательно, фиксированным значениям критериев соответствует не один процесс теплоотдачи, а целая совокупность подобных процессов. Это означает, что если функциональную связь между критериями представить в виде к р и т е р и а л ь н о г о уравнения, полученного в результате обработки экспериментальных данных теплоотдачи, то это уравнение будет справедливо и для других подобных процессов переноса тепла в пограничном слое.

Таким образом, метод теплового подобия дает возможность из дифференциальных уравнений и граничных условий, описывающих теплоотдачу, создать теоретическую основу для постановки опытов и обработки результатов экспериментов при получении критериальных уравнений.

Совершенно очевидно, что теория теплового подобия наиболее плодотворно может быть использована в том случае, когда невозможно аналитическое решение.

7.2.2. Критерии теплового подобия

Под критериями теплового подобия понимают безразмерные комплексы, составленных из определенных комбинаций величин, описывающих тот или иной процесс теплоотдачи.

Ниже приведены критерии, которые наиболее распространены в теории конвективного теплообмена.

Критерий Нуссельта, ,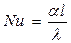

где α – коэффициент теплоотдачи,

l – характерный геометрический размер;

λ – коэффициент теплопроводности

Критерий Нуссельта характеризует теплообмен на границе стенка – теплоноситель и устанавливает численное отношение между интенсивностью теплоотдачи и тепловой проводимостью (λ / l) теплоносителя.

Критерий Рейнольдса,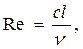

гдеc– скорость теплоносителя;

ν – коэффициент кинематической вязкости.

Критерий Рейнольдса характеризует режим течения теплоносителя и устанавливает соотношение между силами инерции и силами вязкости.

Критерий Прандтля, ,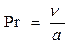

где 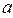– коэффициент температуропроводности.

Критерий Прандтля характеризует физические свойства жидкости, является мерой подобия температурных и скоростных полей в потоке теплоносителя. При Pr = 1 толщины теплового и динамического пограничных слоев равны, т.е. δ_m=δ_д .

Критерий Грасгофа,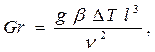

где g – ускорение земного притяжения;

β – коэффициент объемного расширения теплоносителя;

∆T– разность температур между теплоносителем и стенкой.

Критерий Грасгофа характеризует кинематическое подобие при свободном движении теплоносителя и устанавливает соотношение подъемной силы, возникающей вследствие разности плотностей жидкости и силы молекулярного трения.

В ряд критериев подобия входит характерный геометрический размер. В качестве характерного выбирают тот геометрический размер, который определяет развитие процесса течения теплоносителя около поверхности теплоотдачи. Этот размер называют определяющим.

Для труб круглого сечения таким определяющим размером является внутренний диаметр трубы. Для каналов некруглого сечения в качестве определяющего размера выбирается эквивалентный диаметр, который вычисляется по формуле:

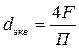, (7.9)

где F – площадь поперечного сечения канала;

П – смоченный периметр нормального сечения канала.

При поперечном обтекании трубы и пучка труб в качестве определяющего размера берется наружный диаметр трубы, а при обтекании плиты - ее длина по направлению движения потока.

Входящие в критерии подобия величины, характеризующие физические свойства теплоносителя, в значительной степени зависят от его температуры. Температура же теплоносителя в процессе теплоотдачи меняется как по толщине пограничного слоя, так и вдоль поверхности теплообмена. Поэтому важно условиться, какую температуру принимать в качестве определяющей для выбора физических параметров.

В инженерной практике за определяющую принимают ту температуру, которая в технических расчетах бывает задана или легко может быть определена в эксперименте. Это либо температура в ядре потока того сечения, для которого вычисляется коэффициент теплоотдачи, либо средняя по длине канала температура теплоносителя.

7.2.3. Критериальные уравнения

Теория теплового подобия позволяет определить величину коэффициента теплоотдачи при помощи соответствующего критериального уравнения.

Критериальным называют уравнение, которое зависимость между величинами, описывающими конвективный теплообмен в дифференциальной или другой форме, представляет зависимостью между критериями подобия.

Так, например, функциональная связь

Nu = f (Re, Gr, Pr) (7.10)

представляет собой критериальное уравнение в общем виде.

Для выявления критериев, входящих в критериальные уравнения и установления функциональной связи между ними, в настоящее время используются в основном два метода: метод масштабных преобразований и метод размерностей. Использование метода масштабных преобразований возможно при условии описания процесса конвективного теплообмена замкнутой системой дифференциальных уравнений с условиями однозначности. Подробно этот метод рассмотрен в работах [4. 6. 10].

Метод размерностей используется, когда рассматривается сложный и новый процесс, для которого еще нет аналитического описания. В этом

случае необходимо установить полный перечень существенных для процесса физических величин, т.е. тех, которые должны войти в дифференциальные уравнения и условия однозначности. Располагая списком размерных величин, можно установить список критериев подобия и вид критериального уравнения.

Пусть, например, установлены факторы, влияющие на коэффициент теплоотдачи в данной системе, т.е α = f ( c, ρ, ν, λ, c_p, d ).

Допустим, что между этими величинами существует степенная функциональная связь вида

α = К с^α ρ^b ν ^f λ^e c_p^r d^g , (7.11)

где K – коэффициент пропорциональности (безразмерная величина).

Размерности обеих частей равенства должны быть одинаковы, т.е.

Дж/(м с К)=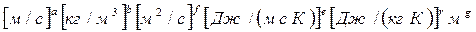

Составив уравнения относительно показателей степеней для каждой размерности, получим систему:

джоуль: 1 = e + r;

метр: - 2 = a - 3b + 2f - e + g;

секунда: - 1 = - a - f – e;

кельвин: - 1 = - e – r;

килограмм: 0 = b – r.

Выразим искомые величины в этой системе через a и b :

r = b

e = 1 – b

f = 1 – a – 1 + b = b - a

g = 2 – a + 3b – 2b + 2a +1 – b = a – 1.

Подставив значения a , b, e , r, и g в уравнение (7.11), получими

:

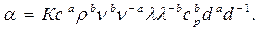
Сгруппировав величины с одинаковыми показателями степеней, выявим безразмерные комплексы:

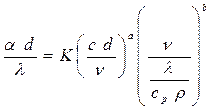
или

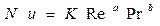(7.12)

Таким образом, используя метод размерностей, можно выявить критерии подобия и вид критериальных уравнений, описывающих подобные процессы теплоотдачи.

Использование критериальных уравнений вида (7.12) возможно, если известны значения величин К, α, b. Для их определения проводится серия опытов по экспериментальному исследованию коэффициента теплоотдачи

с измерением всех величин, входящих в критерии подобия рассматриваемого критериального уравнения. Причем от опыта к опыту параметры, влияющие на значение α, изменяются так, что диапазон изменения критериев становится существенным. Обработка результатов экспериментов ведется графоаналитическим методом. Поясним его сущность.

Предположим, что критерий Nu зависит только от критерия Re , т.е.

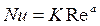^. (7.13)

Из серии экспериментов выбирают опытные данные для нескольких отличающихся друг от друга чисел Re и вычисляют соответствующие им значения Nu. Расположение опытных точек на графике, где по оси ординат отложены значения Nu , а по оси абсцисс – Re, покажет характер зависимости Nu = f (Re). Однако определить значения показателя степени и коэффициента пропорциональности K по полученному графику сложно. Задача упрощается, если выражение (7.13) линеаризировать и использовать логарифмическую систему координат.

Нанесем опытные данные на поле графика с координатами ln Nu

и ln Re , рис. 7.3. Экспериментальные точки расположатся вдоль прямой линии 1-2, которая представлена выражением (7.13) в логарифмическом виде:

ln Nu = ln K + ln Re.

Отсюда показатель степени числа Re для выражения (7.13) вычисляется как отношение катетов, т.е.

.

Коэффициент пропорциональностиопределяется из соотношения:

Рис.7.3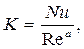

которому удовлетворяет любая точка прямой, (см. рис.7.3).

Eсли искомая величина Nu является функцией двух аргументов, например Nu = f(Re, Pr), то сначала при фиксированном значении Pr строят график и по нему определяют показатель при числе Re. Затем опытные данные представляют на графике в виде зависимости:

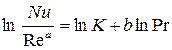
и определяют показатель степени b. Величину K находят из соотношения:

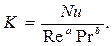
Полученные таким образом критериальные уравнения являются чисто эмпирическими. Они применимы для подобных явлений теплообмена лишь в тех пределах изменения критериев, в которых подтверждены опытом. Экстраполяция этих уравнений на большие или меньшие значения критериев, строго говоря, недопустима.